题目内容
已知函数f(x)=lnx+ax+1,a∈R.
(Ⅰ)求f(x)在x=1处的切线方程;
(Ⅱ)若不等式f(x)≤0恒成立,求a的取值范围;
(Ⅲ)数列{an}中,a1=2,2an+1=an+1,数列{bn}满足bn=nlnan,记{bn}的前n项和为Tn.求证:Tn<4-
.
(Ⅰ)求f(x)在x=1处的切线方程;
(Ⅱ)若不等式f(x)≤0恒成立,求a的取值范围;
(Ⅲ)数列{an}中,a1=2,2an+1=an+1,数列{bn}满足bn=nlnan,记{bn}的前n项和为Tn.求证:Tn<4-
| n+2 |
| 2n-1 |
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用,数列的求和
专题:导数的综合应用,点列、递归数列与数学归纳法
分析:(Ⅰ)求出原函数的导函数,得到函数在x=1时的导数,再求出f(1),然后直接利用直线方程的点斜式得答案;
(Ⅱ)由f(x)≤0恒成立分离参数a,然后构造函数g(x)=
,由导数求其最小值,则实数a的取值范围可求;
(Ⅲ)由递推式求出数列{an}的通项公式,借助于函数y=x-ln(1+x)在(0,1]上单调性及不等式放缩证明Tn<4-
.
(Ⅱ)由f(x)≤0恒成立分离参数a,然后构造函数g(x)=
| -lnx-1 |
| x |
(Ⅲ)由递推式求出数列{an}的通项公式,借助于函数y=x-ln(1+x)在(0,1]上单调性及不等式放缩证明Tn<4-
| n+2 |
| 2n-1 |
解答:
(Ⅰ)解:由f(x)=lnx+ax+1,得f′(x)=
+a.
∴f′(1)=1+a.
又f(1)=a+1,
∴f(x)在x=1处的切线方程为y-a-1=(1+a)(x-1),
即y=(1+a)x;
(Ⅱ)解:函数f(x)=lnx+ax+1的定义域为{x|x>0},
由不等式f(x)≤0恒成立,得
lnx+ax+1<0恒成立,即a<
(x>0)恒成立.
令g(x)=
,
则g′(x)=
=
,
当0<x<1时,g′(x)<0,g(x)为减函数,当x>1时,g′(x)>0.
∴g(x)min=g(1)=-1.
∴使不等式f(x)≤0恒成立的a的取值范围是(-∞,-1);
(Ⅲ)证明:∵a1=2,2an+1=an+1,
∴2(an+1-1)=an-1,
则数列{an-1}是以a1-1=1为首项,以
为公比的等比数列,
∴an-1=(
)n-1,即an=1+(
)n-1.
下面证明当0<x≤1时,x-ln(1+x)>0,
设y=x-ln(1+x),则y′=1-
,
∵对于任意x∈(0,1]均有y′<0,
∴y=x-ln(1+x)在(0,1]上单调递减,
∵当x=1时y=x-ln(1+x)=1-ln2>0,
∴当0<x≤1时,x-ln(1+x)>0.
记Cn=n•(
)n-1,Sn=
Ci,
显然有bn=n•ln[1+(
)n-1]<n•(
)n-1=Cn.
∴Tn=
bi<
Ci=Sn,
∵Sn=
Ci=
i(
)i-1,
而对任意n∈N*都有2-
≥0,
∴Tn<Sn=4-
.
| 1 |
| x |
∴f′(1)=1+a.
又f(1)=a+1,
∴f(x)在x=1处的切线方程为y-a-1=(1+a)(x-1),
即y=(1+a)x;
(Ⅱ)解:函数f(x)=lnx+ax+1的定义域为{x|x>0},
由不等式f(x)≤0恒成立,得
lnx+ax+1<0恒成立,即a<
| -lnx-1 |
| x |
令g(x)=
| -lnx-1 |
| x |
则g′(x)=
| -1+lnx+1 |
| x2 |
| lnx |
| x2 |
当0<x<1时,g′(x)<0,g(x)为减函数,当x>1时,g′(x)>0.
∴g(x)min=g(1)=-1.
∴使不等式f(x)≤0恒成立的a的取值范围是(-∞,-1);
(Ⅲ)证明:∵a1=2,2an+1=an+1,
∴2(an+1-1)=an-1,
则数列{an-1}是以a1-1=1为首项,以
| 1 |
| 2 |
∴an-1=(
| 1 |
| 2 |
| 1 |
| 2 |
下面证明当0<x≤1时,x-ln(1+x)>0,
设y=x-ln(1+x),则y′=1-
| 1 |
| 1+x |
∵对于任意x∈(0,1]均有y′<0,
∴y=x-ln(1+x)在(0,1]上单调递减,
∵当x=1时y=x-ln(1+x)=1-ln2>0,
∴当0<x≤1时,x-ln(1+x)>0.
记Cn=n•(
| 1 |
| 2 |
| n |
 |
| i=1 |
显然有bn=n•ln[1+(
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=
| n |
 |
| i=1 |
| n |
 |
| i=1 |
∵Sn=
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| 1 |
| 2 |
而对任意n∈N*都有2-
| 2 |
| 2n-1 |
∴Tn<Sn=4-
| n+2 |
| 2n-1 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了利用放缩法证明数列不等式,综合考查了学生的逻辑思维能力和分析解决问题的能力,是压轴题.

练习册系列答案
相关题目
设集合A={1,2,3,4,5},集合B={1,3,5},则集合A∩B=( )
| A、{2,4} |
| B、{1,2,3} |
| C、{1,3,5} |
| D、{1,2,3,4,5} |
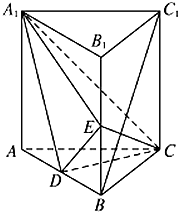 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=