题目内容
4.已知$\frac{π}{3}$是函数f(x)=2cos2x+asin2x+1的一个零点.(Ⅰ)求实数a的值;
(Ⅱ)求f(x)的单调递增区间.
分析 (Ⅰ)利用函数的零点的定义,求得实数a的值.
(Ⅱ)利用三角恒等变化化简函数的解析式,再利用正弦函数的单调性求得f(x)的单调递增区间.
解答 解:(Ⅰ)由题意可知$f(\frac{π}{3})=0$,即$f(\frac{π}{3})=2{cos^2}\frac{π}{3}+asin\frac{2π}{3}+1=0$,
即$f(\frac{π}{3})=2{(\frac{1}{2})^2}+\frac{{\sqrt{3}}}{2}a+1=0$,解得$a=-\sqrt{3}$.
(Ⅱ)由(Ⅰ)可得$f(x)=2{cos^2}x-\sqrt{3}sin2x+1$=$cos2x-\sqrt{3}sin2x+2$=$2sin(2x+\frac{5π}{6})+2$,
函数y=sinx的递增区间为$[{2kπ-\frac{π}{2},2kπ+\frac{π}{2}}]$,k∈Z.
由$2kπ-\frac{π}{2}<2x+\frac{5π}{6}<2kπ+\frac{π}{2}$,k∈Z,
得$kπ-\frac{2π}{3}<x<kπ-\frac{π}{6}$,k∈Z,
所以,f(x)的单调递增区间为$[{kπ-\frac{2π}{3},kπ-\frac{π}{6}}]$,k∈Z.
点评 本题主要考查函数的零点的定义,三角恒等变换、正弦函数的单调性,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
14.已知两正数x,y 满足x+y=1,则z=$(x+\frac{1}{x})(y+\frac{1}{y})$的最小值为( )
| A. | $\frac{33}{4}$ | B. | $\frac{25}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{17}}}{4}$ |
16.已知椭圆:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3),左右焦点分别为F1,F2,过F1的直线l交椭圆于A、B两点,若|BF2|+|AF2|的最大值为10,则b的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
13.函数y=sin2(x-$\frac{π}{4}$)的图象沿x轴向右平移m个单位(m>0),所得图象关于y轴对称,则m的最小值为( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
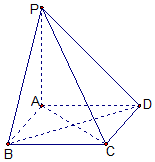 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.