Question

如图，已知PA是⊙O的切线，A为切点．PC是⊙O的一条割线，交⊙O于B，C两点，点Q是弦BC的中点．若圆心O在∠APB内部，则∠OPQ+∠PAQ的度数为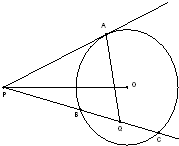

 

．

Answer 1

考点：弦切角

专题：直线与圆

分析：连结AO，QO，由已知条件推导出OA⊥PA，OQ⊥PQ，从而得到A，P，Q，O四点共圆，由此能求出∠OPQ+∠PAQ的值．

解答： 解：连结AO，QO，
∵PA是⊙O的切线，A为切点．
PC是⊙O的一条割线，交⊙O于B，C两点，点Q是弦BC的中点，
∴OA⊥PA，OQ⊥PQ，
∴∠PAO+∠PQO=180°，
∴A，P，Q，O四点共圆，
∴∠OPQ=∠OAQ，
∵∠OAQ+PAQ=90°，
∴∠OPQ+∠PAQ=90°．
故答案为：90°．

点评：本题考查两角和的求法，是中档题，解题时要注意四点共圆的证明及其应用．