题目内容
6.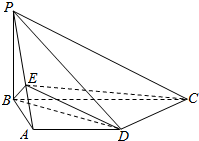 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.(1)若PC∥平面BDE,求实数λ的值,
(2)在(1)的条件下,求三棱锥B-EDC的体积.
分析 (1)连结AC交BD于F,连结EF,由线面平行的性质得PC∥EF,故而$\frac{PE}{EA}=\frac{FC}{FA}$,由于底面为直角梯形,AB=AD,BD⊥CD可得△BCD是等腰直角三角形,从而求出BC,于是$\frac{FC}{FA}=\frac{BC}{AD}$;
(2)求出E到底面的距离和△BCD的面积即可求出棱锥的体积.
解答 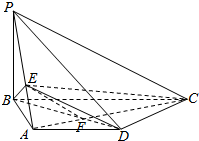 解:(1)连结AC交BD于F,连结EF,
解:(1)连结AC交BD于F,连结EF,
∵PC∥平面BDE,PC?平面APC,平面APC∩平面BDE=EF,
∴PC∥EF,∴$\frac{PE}{EA}=\frac{FC}{FA}$.
∵四边形ABCD是直角梯形,AD∥BC,CD⊥BD,
∴AB⊥AD,AB⊥BC,
∵AB=AD=3,∴BD=3$\sqrt{2}$,∠ABD=∠ADB=45°,
∴∠DBC=45°,又∵BD⊥CD,
∴△BCD是等腰直角三角形,∴BC=$\sqrt{2}$BD=6.
∵AD∥BC,∴△ADF∽△CFB,
∴$\frac{FC}{FA}=\frac{BC}{AD}$=$\frac{6}{3}$=2.
∴λ=2.
(2)∵$\frac{PE}{EA}=2$,PB⊥平面ABCD,
∴E到底面ABCD的距离h=$\frac{1}{3}$PB=1.
∴三棱锥B-EDC的体积V=V棱锥E-BCD=$\frac{1}{3}$×$\frac{1}{2}$×BD×CD×h=$\frac{1}{3}×\frac{1}{2}×3\sqrt{2}×3\sqrt{2}×1$=3.
点评 本题考查了线面平行的性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
17.已知顶点在原点,关于y轴对称的抛物线与直线x-2y=1交于P,Q两点,若|PQ|=$\sqrt{15}$,则抛物线的方程为( )
| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |
15.直线a∥平面α,直线b⊥平面α,则下列说法正确的是( )
| A. | a∥b | B. | a⊥b | C. | a⊥b且异面 | D. | a⊥b且相交 |
16.某产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:
(1)求y与x之间的回归直线方程;(参考数据:22+42+52+62+82=145,2×30+4×40+5×60+6×50+8×70=1380)
(2)试预测广告费用支出为1千万元时,销售额是多少?
附:线性回归方程y=bx+a中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值,线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费用支出为1千万元时,销售额是多少?
附:线性回归方程y=bx+a中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值,线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
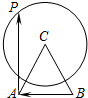 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].