题目内容
17.已知顶点在原点,关于y轴对称的抛物线与直线x-2y=1交于P,Q两点,若|PQ|=$\sqrt{15}$,则抛物线的方程为( )| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |
分析 设出抛物线的方程,直线与抛物线方程联立消去y,进而根据韦达定理求得x1+x2的值,进而利用弦长公式求得|PQ|,利用|PQ|=$\sqrt{15}$,则抛物线的方程可得.
解答 解:设抛物线的方程为x2=2ay,则
抛物线与直线x-2y=1,消去y得x2-ax+a=0,x1•x2=a,x1+x2=a
|PQ|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+\frac{1}{4}}$•$\sqrt{{a}^{2}-4a}$=$\sqrt{15}$,
∴a2-4a-12=0,a=-2,或6
∴x2=-4y或x2=12y.
故选:C.
点评 本题主要考查了抛物线的标准方程.解题的关键是对抛物线基本性质和标准方程的熟练应用.

练习册系列答案
相关题目
7.执行如图所示的程序框图,若输入n的值为3,则输出S的值为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.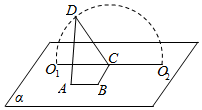 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
7.过点P(2,3)作圆(x+4)2+(y+1)2=9的切线PA,PB,切点分别是A,B,则直线AB的方程为( )
| A. | 6x+4y+19=0 | B. | 4x-6y+19=0 | C. | 6x-4y+19=0 | D. | 4x+6y-19=0 |
 任取实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于79的概率是$\frac{3}{4}$.
任取实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于79的概率是$\frac{3}{4}$.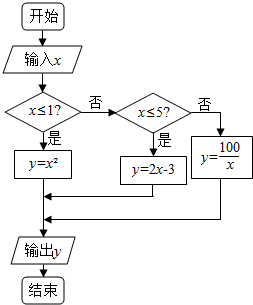 如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.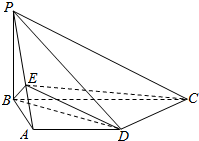 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.