题目内容
18.直线l过抛物线C:y2=2px(p>0)的焦点F且与C相交于A,B两点,且AB的中点M的坐标为(3,2),则抛物线C的方程为y2=4x或y2=8x.分析 先利用点差法,求出AB的斜率,可得直线AB的方程为y=$\frac{p}{2}$(x-$\frac{p}{2}$),代入y2=2px,利用中点坐标公式,即可得出抛物线C的方程.
解答 解:抛物线y2=2px的焦点为F($\frac{p}{2}$,0)
设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
两式相减可得:y12-y22=2p(x1-x2),
∴kAB=$\frac{2p}{{y}_{1}+{y}_{2}}$=$\frac{p}{2}$,
直线AB的方程为y=$\frac{p}{2}$(x-$\frac{p}{2}$),代入y2=2px,可得4px2-(4p2+32)x+p3=0
可得x1+x2=$\frac{{p}^{2}+8}{p}$=6,解之得p=2或4,
∴物线C的方程为y2=4x或y2=8x.
故答案为:y2=4x或y2=8x.
点评 本题考查抛物线C的方程,考查点差法,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.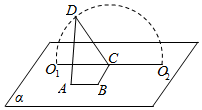 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
10.下列函数,在其定义域内,既是减函数又是奇函数的是( )
| A. | $y={({\frac{1}{2}})^x}$ | B. | $y={2^{{{log}_2}x}}$ | C. | y=2x | D. | $y={log_2}{2^{-x}}$ |
7.过点P(2,3)作圆(x+4)2+(y+1)2=9的切线PA,PB,切点分别是A,B,则直线AB的方程为( )
| A. | 6x+4y+19=0 | B. | 4x-6y+19=0 | C. | 6x-4y+19=0 | D. | 4x+6y-19=0 |
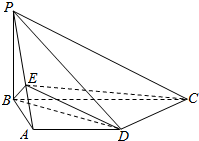 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.