题目内容
1．随着学习的深入我们发现很多对事物的看法已经颠覆了我们传统的认识，例如直线与曲线有且只有一个交点并不能说直线是曲线的切线，曲线的切线与曲线的切点也不一定只有一个．若在曲线f（x，y）=0上两个不同点处的切线重合，则称这条切线为曲线f（x，y）=0的“自公切线”．下列方程：①x2-y2=1；②y=x2-|x|，③y=3sinx+4cosx；④|x|+1=$\sqrt{4-{y}^{2}}$对应的曲线中存在“自公切线”的有（ ）| A． | ①② | B． | ③④ | C． | ①④ | D． | ②③ |
分析 ①x2-y2=1 是一个等轴双曲线，没有自公切线；
②在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$，故②有自公切线；
③此函数是周期函数，过图象的最高点的切线都重合或过图象的最低点的切线都重合，此函数有自公切线；
④结合图象可得，此曲线没有自公切线．
解答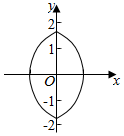 
解：①x2-y2=1 是一个等轴双曲线，没有自公切线；
②y=x2-|x|=$\left\{\begin{array}{l}{（x-\frac{1}{2}）^{2}-\frac{1}{4}，x≥0}\\{（x+\frac{1}{2}）^{2}-\frac{1}{4}，x＜0}\end{array}\right.$，
在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$，故②有自公切线；
③y=3sinx+4cosx=5sin（x+φ），cosφ=$\frac{3}{5}$，sinφ=$\frac{4}{5}$，此函数是周期函数，
过图象的最高点的切线都重合或过图象的最低点的切线都重合，故此函数有自公切线；
④由于|x|+1=$\sqrt{4-{y}^{2}}$，即x2+2|x|+y2-3=0，图象如右，结合图象可得，此曲线没有自公切线．
故选：D．
点评 正确理解新定义“自公切线”，正确画出函数的图象、数形结合的思想方法是解题的关键．
练习册系列答案
相关题目
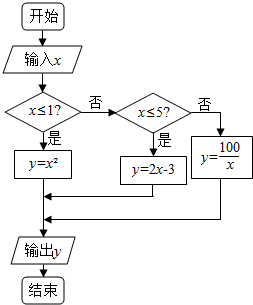如图，给出了一个程序框图，其作用是输入x的值，输出相应y的值．
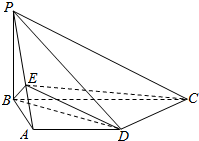如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，CD⊥BD，PB⊥平面ABCD，PB=AB=AD=3，点E在线段PA上，且满足$\frac{PE}{EA}$=λ．
10．下列函数，在其定义域内，既是减函数又是奇函数的是（ ）
| A． | $y={（{\frac{1}{2}}）^x}$ | B． | $y={2^{{{log}_2}x}}$ | C． | y=2x | D． | $y={log_2}{2^{-x}}$ |