若角α的终边经过点P.则sin2α=-$\frac{4}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．若角α的终边经过点P（-1，2），则sin2α=-$\frac{4}{5}$．

分析利用三角函数的定义，计算α的正弦与余弦值，再利用二倍角公式，即可求得结论．

解答解：由题意，|OP|=$\sqrt{5}$，∴sinα=$\frac{2}{\sqrt{5}}$，cosα=-$\frac{1}{\sqrt{5}}$，
∴sin2α=2sinαcosα=2×$\frac{2}{\sqrt{5}}$×（-$\frac{1}{\sqrt{5}}$）=-$\frac{4}{5}$，
故答案为：-$\frac{4}{5}$．

点评本题考查三角函数的定义，考查二倍角公式，属于基础题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

5．

任取实数x∈[2，30]，执行如图所示的程序框图，则输出的x不小于79的概率是$\frac{3}{4}$．

2．函数f（x）=e^x-2x+a，若关于x的方程f（x）=0有两个不同正根，则实数a的取值范围是（-1，2ln2-2）．

9．已知|$\overrightarrow{a}$|=1，$\overrightarrow{b}$=（1，$\sqrt{3}$），（$\overrightarrow{b}$-$\overrightarrow{a}$）⊥$\overrightarrow{a}$，则向量a$\overrightarrow{\;}$与向量$\overrightarrow{b}$的夹角为$\frac{π}{3}$．

19．已知直线y=kx+m（m≠0）与圆x²+y²=169有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有（　　）

6．

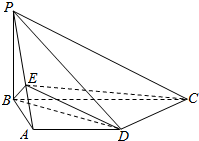如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，CD⊥BD，PB⊥平面ABCD，PB=AB=AD=3，点E在线段PA上，且满足$\frac{PE}{EA}$=λ．
（1）若PC∥平面BDE，求实数λ的值，
（2）在（1）的条件下，求三棱锥B-EDC的体积．

3．已知$f（x）=2sin（{x+\frac{π}{3}}）（{x∈R}）$，函数y=f（x+φ）（|φ|≤$\frac{π}{2}$）的图象关于直线x=0对称，则φ的值为$\frac{π}{6}$．

4．函数f（x）=lnx+x²-10的零点所在的区间为（　　）

试题分类