题目内容

20．求下列函数的导数．
（1）y=（x+1）（x+2）（x+3）
（2）y=2x•tanx．

分析 （1）先将函数的解析式变形可得y=x3+6x2+11x+6，对其求导即可得答案；
（2）由同角三角函数的基本关系式分析可得y=$\frac{2xsinx}{cosx}$，利用商的导数计算公式计算可得答案．

解答 解：（1）y=（x+1）（x+2）（x+3）=x3+6x2+11x+6，
则其导数y′=3x2+12x+11；
（2）y=2x•tanx=$\frac{2xsinx}{cosx}$，
其导数y′=（$\frac{2xsinx}{cosx}$）′=2×$\frac{（xsinx）′cosx-xsinx（cosx）′}{co{s}^{2}x}$=$\frac{2sinxcosx+2x}{co{s}^{2}x}$．

点评 本题考查导数的计算，关键是牢记导数计算的公式以及运算方法．

练习册系列答案
相关题目
5．已知函数f（x）=（x+m）lnx-（m+1+$\frac{1}{e}$）x在x=e处取到极值
（Ⅰ）求m的值
（Ⅱ）当x＞1时，证明f（x）+（2+$\frac{1}{e}$）x＞2x-2
（Ⅲ）如果s，t，r满足|s-r|≤|t-r|，那么称s比t更靠近r，当a≥2且x≥1时，试比较$\frac{e}{x}$和ex-1+a哪个更靠近f（x），并说明理由．
11．如果函数f（x）=3cos（2x+$\frac{π}{6}$），则f（x）的图象（　　）
A．关于点（-$\frac{π}{12}$，0）对称B．关于点（$\frac{π}{6}$，0）对称
C．关于直线x=$\frac{π}{6}$对称D．关于直线x=$\frac{π}{2}$对称
8．如图是正方体的侧面展开图，l1、l2是两条侧面对角线，则在此正方体中，l1与l2（　　）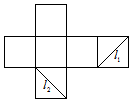
A．互相平行B．相交且夹角为$\frac{π}{3}$C．异面且互相垂直D．异面且夹角为$\frac{π}{3}$
15．已知命题$p：?{x_0}∈R，使x_0^2+{x_0}+1＜0，命题q：?a∈R，若b＞c，则ab＞ac$，给出下列结论：
①命题“p∧q”是真命题
②命题“p∨q”是真命题
③命题“（?p）∨q”是真命题
④命题“（?p）∧（?q）”是真命题
其中正确的是（　　）
A．①③B．①④C．②③D．③④
5．已知f（x）=4x5+3x4+2x3-x2-x-$\frac{1}{2}$，用秦九韶算法求f（-2）等于（　　）
A．-$\frac{197}{2}$B．$\frac{197}{2}$C．$\frac{183}{2}$D．-$\frac{183}{2}$
12．已知a＞0，函数f（x）=ax-x2．求f（x）≤1，x∈[0，1]恒成立的充要条件．
9．在数列{an}中，若a1=-2，且对任意的n∈N*有an+1=1+an，则数列{an}前10项的和为（　　）
A．5B．10C．25D．30
10．若zl=a+2i，z2=3-4i，且$\frac{z_1}{z_2}$为实数，则实数a的值为$-\frac{3}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网