题目内容
2.已知函数f(x)=|x-a|-|x+1|,a∈R.(Ⅰ)当a=1时,求不等式f(x)≤x2-x的解集;
(Ⅱ)若正实数m,n满足2m+n=1,函数$f(x)≤\frac{1}{m}+\frac{2}{n}$恒成立,求实数a的取值范围.
分析 (Ⅰ)通过讨论x的范围,求出不等式的解集即可;(Ⅱ)求出$\frac{1}{m}$+$\frac{2}{n}$的最小值,问题转化为|a+1|≤8,解出即可.
解答 解:(Ⅰ)a=1时,f(x)=|x-1|-|x+1|,
f(x)≤x2-x即|x-1|-|x+1|≤x2-x,
x≥1时,x-1-x-1≤x2-x,即x2-x+2≥0,
解得:x≥2或x≤-1,(舍),
-1<x<1时,1-x-x-1≤x2-x,即x2+x≥0,解得:x≥0或x≤-1(舍),
x≤-1时,1-x+x+1≤x2-x,即x2-x-2≥0,
解得:x≥2(舍)或x≤-1,
综上,不等式的解集是(-∞,-1]∪[0,+∞);
(Ⅱ)若正实数m,n满足2m+n=1,
则$\frac{1}{m}$+$\frac{2}{n}$=($\frac{1}{m}$+$\frac{2}{n}$)(2m+n)=4+$\frac{n}{m}$+$\frac{4m}{n}$≥4+2$\sqrt{\frac{n}{m}•\frac{4m}{n}}$=8,
当且仅当n=2m即n=$\frac{1}{2}$,m=$\frac{1}{4}$时“=”成立,
函数$f(x)≤\frac{1}{m}+\frac{2}{n}$恒成立,即|x-a|-|x+1|≤|x-a-x-1|=|a+1|≤8,
解得:-9≤a≤7.
点评 本题考查了绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
7.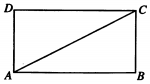 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
14.具有线性相关关系的变量x、y的一组数据如表所示.若y与
x的回归直线方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$,则m的值是( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 6 |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5.5 | D. | 6 |
11.从1、2、3、4、5、6这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为( )
| A. | 300 | B. | 216 | C. | 180 | D. | 162 |
 已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )
已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )