题目内容
若定义一种新运算a?b=
，求函数f（x）=x?（3-x）的值域．
|
考点：函数的值域
专题：新定义
分析：这是一个新定义运算问题，取两者中较小的一个．借助函数图象能比较直观的判断出．
解答：
解：f(x)=
∵当x∈[
，+∞)时，f（x）单调递减，当x∈(-∞，
)时，f（x）单调递增，
∴f(x)≥f(
)=
，∴函数的值域为[
，+∞)．
故答案为：[
，+∞)．
|
| 3 |
| 2 |
| 3 |
| 2 |
∴f(x)≥f(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为：[
| 3 |
| 2 |
点评：分断函数的值域，是每段值域的并集．
练习册系列答案
相关题目
下列命题中正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x≥0” |
| C、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
| D、命题“p∧q为真”是命题“p∨q为真”的必要不充分条件 |
定义在R上的奇函数满足f（x+1）=-f（1-x），当x∈（0，1）时，f（x）=log
（1-x），则f（x）在（1，2）上（ ）
| 1 |
| 2 |
| A、是减函数，且f（x）＞0 |
| B、是增函数，且f（x）＜0 |
| C、是减函数，且f（x）＜0 |
| D、是增函数，且f（x）＞0 |
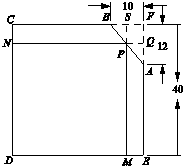有一块铁皮零件，它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE，其中AF长等于12cm，BF长等于10cm，如图所示．现在需要截取矩形铁皮，使得矩形相邻两边在CD，DE上．请问如何截取，可以使得到的矩形面积最大？（图中单位：cm）
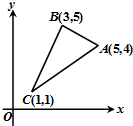如图，已知可行域为△ABC及其内部，若目标函数z=kx+y当且仅当在点B处取得最大值，则k的取值范围是