题目内容
某几何体三视图如下图所示,则该几何体的体积是( )


A、1+
| ||
B、1+
| ||
C、1+
| ||
| D、1+π |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据三视图判断知几何体是正方体与
圆锥的组合体,且圆锥的高为4,底面半径为1;正方体的边长为1,把数据代入圆锥与正方体的体积公式计算可得答案.
| 1 |
| 4 |
解答:
解:由三视图知几何体的下部是正方体,上部是
圆锥,且圆锥的高为4,底面半径为1;
正方体的边长为1,
∴几何体的体积V=V正方体+V
圆锥=13+
×
×π×12×1=1+
.
故选:A.
| 1 |
| 4 |
正方体的边长为1,
∴几何体的体积V=V正方体+V
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| π |
| 12 |
故选:A.
点评:本题考查了由三视图求几何体的体积,解答此类问题的关键是判断几何体的形状及图中数据所对应的几何量.

练习册系列答案
相关题目
已知x,y满足
,且x2+y2的最小值为8,则正实数a的取值范围是( )
|
| A、(0,2] |
| B、[2,5] |
| C、[3,+∞) |
| D、(0,5] |
下列说法中正确的是( )
| A、若命题p为:对?x∈R有x2>0,则¬p:?x∈R使x2≤0 | ||||
B、若命题p为:
| ||||
| C、若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | ||||
D、方程ax2+x+a=0有唯一解的充要条件是:a=±
|
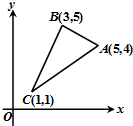 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
