题目内容
某高校进行自主招生面试时的程序如下:共设3道题,每道题答对给10分,答错倒扣5分(每道题都必须回答,但相互不影响).设某学生对每道题答对的概率都为
,则该学生在面试时得分的期望为 .
| 3 |
| 4 |
考点:离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:设该生在面试时的得分为X,由题设条件知X的可能取值为-15,0,15,30,分别求出P(X=-15),P(X=0),P(X=15),P(X=30),由此能求出该学生在面试时得分的期望值.
解答:
解:设该生在面试时的得分为X,由题设条件知X的可能取值为-15,0,15,30,
P(X=-15)=
•(
)3=
,
P(X=0)=
(
)2•
=
,
P(X=15)=
•
•(
)2=
,
P(X=30)=
(
)3=
,
∴EX=-15×
+0×
+15×
+30×
=
.
∴该学生在面试时得分的期望值为
分.
故答案为:
.
P(X=-15)=
| C | 3 3 |
| 1 |
| 4 |
| 1 |
| 64 |
P(X=0)=
| C | 1 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
P(X=15)=
| C | 2 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 64 |
P(X=30)=
| C | 0 3 |
| 3 |
| 4 |
| 27 |
| 64 |
∴EX=-15×
| 1 |
| 64 |
| 9 |
| 64 |
| 27 |
| 64 |
| 27 |
| 64 |
| 75 |
| 4 |
∴该学生在面试时得分的期望值为
| 75 |
| 4 |
故答案为:
| 75 |
| 4 |
点评:本题考查离散型随机变量的数学期望的求法,解题时要认真审题,注意n次独立重复试验中事件恰好发生k次的概率计算公式的灵活运用.

练习册系列答案
相关题目
定义在R上的奇函数满足f(x+1)=-f(1-x),当x∈(0,1)时,f(x)=log
(1-x),则f(x)在(1,2)上( )
| 1 |
| 2 |
| A、是减函数,且f(x)>0 |
| B、是增函数,且f(x)<0 |
| C、是减函数,且f(x)<0 |
| D、是增函数,且f(x)>0 |
下列说法中正确的是( )
| A、若命题p为:对?x∈R有x2>0,则¬p:?x∈R使x2≤0 | ||||
B、若命题p为:
| ||||
| C、若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | ||||
D、方程ax2+x+a=0有唯一解的充要条件是:a=±
|
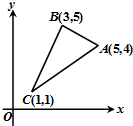 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是