题目内容
已知M（0，
），N（0，-
），G（x，y），直线MG与NG的斜率之积等于-
．
（Ⅰ）求点G的轨迹Γ的方程；
（Ⅱ）过点P（0，3）作一条与轨迹Γ相交的直线l．设交点为A，B．若点A，B均位于y轴的右侧，且
=
，请求出x轴上满足|QP|=|QB|的点Q的坐标．
| 3 |
| 3 |
| 3 |
| 4 |
（Ⅰ）求点G的轨迹Γ的方程；
（Ⅱ）过点P（0，3）作一条与轨迹Γ相交的直线l．设交点为A，B．若点A，B均位于y轴的右侧，且
| BA |
| AP |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由直线MG与NG的斜率之积等于-
，得
•
=-
，由此能求出得点G的轨迹Γ的方程．
（Ⅱ）设直线l的方程为y=kx+3，联立方程组
，得（4k2+3）x2+24kx+24=0，由此利用韦达定理结合已知条件能求出点Q的坐标．
| 3 |
| 4 |
y-
| ||
| x |
y+
| ||
| x |
| 3 |
| 4 |
（Ⅱ）设直线l的方程为y=kx+3，联立方程组
|
解答：
解：（Ⅰ）∵M（0，
），N（0，-
），G（x，y），
∴kMG=
，kNG=
，x≠0，
∵直线MG与NG的斜率之积等于-
，
∴
•
=-
，x≠0，
化简，得点G的轨迹Γ的方程为：
+
=1．（x≠0）
（Ⅱ）设直线l的方程为y=kx+3，k＜0
A（x1，y1），B（x2，y2），（x1＞0，x2＞0），
∵
=
，P（0，3），∴x2=2x1，①
联立方程组
，得（4k2+3）x2+24kx+24=0，（*）
∴x1+x2=
，②，x1x2=
，③
由①得x1x2=
(x1+x2)2，又由②③得(
)2=
，
∴k2=
，k=±
，
∵x1＞0，x2＞0，∴x1+x2=
＞0，
k＜0，∴k=-
，
当k=-
时，方程（*）化为x2-3x+2=0，
解得x1=1，x2=2，∴B（2，0），A（1，
），
设Q（m，0），∵|QP|=|QB|，∴m2+9=（m-2）2，解得m=-
，
∴Q（-
，0）．
| 3 |
| 3 |
∴kMG=
y-
| ||
| x |
y+
| ||
| x |
∵直线MG与NG的斜率之积等于-
| 3 |
| 4 |
∴
y-
| ||
| x |
y+
| ||
| x |
| 3 |
| 4 |
化简，得点G的轨迹Γ的方程为：
| x2 |
| 4 |
| y2 |
| 3 |
（Ⅱ）设直线l的方程为y=kx+3，k＜0
A（x1，y1），B（x2，y2），（x1＞0，x2＞0），
∵
| BA |
| AP |
联立方程组
|
∴x1+x2=
| -24k |
| 4k2+3 |
| 24 |
| 4k2+3 |
由①得x1x2=
| 2 |
| 9 |
| -8k |
| 4k2+3 |
| 12 |
| 4k2+3 |
∴k2=
| 9 |
| 4 |
| 3 |
| 2 |
∵x1＞0，x2＞0，∴x1+x2=
| -24k |
| 4k2+3 |
k＜0，∴k=-
| 3 |
| 2 |
当k=-
| 3 |
| 2 |
解得x1=1，x2=2，∴B（2，0），A（1，
| 3 |
| 2 |
设Q（m，0），∵|QP|=|QB|，∴m2+9=（m-2）2，解得m=-
| 5 |
| 4 |
∴Q（-
| 5 |
| 4 |
点评：本题考查轨迹方程的求法，考查点的坐标的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
（文科）sin
π等于（ ）
| 2009 |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥E-GAC的体积比
为（ ）
| VD-GAC |
| VE-GAC |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
将半径分别为2和1的两个球完全装入底面边长为4的正四棱柱容器中，则该容器的高至少为（ ）
| A、6 | ||
B、3+2
| ||
C、3+
| ||
D、3+
|
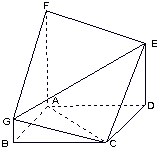如图，多面体ABCDEFG中，FA⊥平面ABCD，FA∥BG∥DE，BG=