题目内容
已知数列{an}的前n项和为Sn，并满足an+2=2an+1-an，a6=4-a4，则S9= ．
考点：数列的求和
专题：等差数列与等比数列
分析：由已知条件推导出数列{an}是等差数列，由此利用等差数列性质能求出结果．
解答：
解：∵数列{an}的前n项和为Sn，并满足an+2=2an+1-an，
∴数列{an}是等差数列，
∵a6=4-a4，∴a6+a4=4，
∴S9=
(a6+a4)=
×4=18．
故答案为：18．
∴数列{an}是等差数列，
∵a6=4-a4，∴a6+a4=4，
∴S9=
| 9 |
| 2 |
| 9 |
| 2 |
故答案为：18．
点评：本题考查数列的前9项和的求法，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
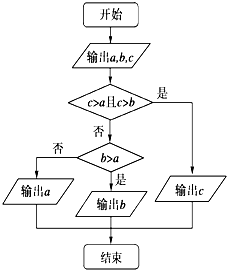如图程序框图表示的算法是（ ）| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
函数f（x）=cos3x+sin2x-cosx，在[0，2π）上的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|