题目内容
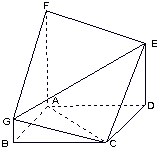 如图,多面体ABCDEFG中,FA⊥平面ABCD,FA∥BG∥DE,BG=
如图,多面体ABCDEFG中,FA⊥平面ABCD,FA∥BG∥DE,BG=| 1 |
| 4 |
| 3 |
| 4 |
(1)求证:GC∥平面ADEF;
(2)求二面角C-GE-D余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件得平面BGC∥平面ADEF,由此能证明GC∥平面ADEF.
(2)以A为原点,以射线AB、AD、AF分别为x轴、y轴、z轴建立空间直角坐标系,利用向量法能求出二面角C-GE-D余弦值.
(2)以A为原点,以射线AB、AD、AF分别为x轴、y轴、z轴建立空间直角坐标系,利用向量法能求出二面角C-GE-D余弦值.
解答:
(本小题满分12分)
 (1)证明:∵FA∥BG,BC∥AD,BG∩BC=B,AF∩AD=A,
(1)证明:∵FA∥BG,BC∥AD,BG∩BC=B,AF∩AD=A,
∴平面BGC∥平面ADEF
又GC?平面BGC,
∴GC∥平面ADEF.…(5分)
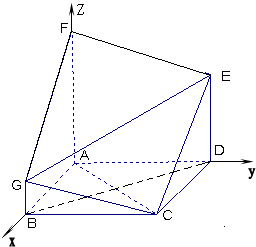
(2)解:以A为原点,以射线AB、AD、AF分别为x轴、y轴、
z轴建立如图所示的坐标系,
不妨令AB=AF=4,则BG=1,DE=3,
∴G(4,0,1),C(4,4,0),E(0,4,3),
=(0,-4,1),
=(-4,0,3),
令
=(x,y,z),
⊥平面CGE,
则
⇒
⇒
⇒
不妨令y=1,则
=(3,1,4),
又AC⊥平面BDEG,则平面BDEG的一个法向量为
=(4,4,0)
设二面角C-GE-D的大小为θ,由图得θ为锐角,
∴cosθ=
=
=
.
∴二面角C-GE-D余弦值为
.…(12分)
 (1)证明:∵FA∥BG,BC∥AD,BG∩BC=B,AF∩AD=A,
(1)证明:∵FA∥BG,BC∥AD,BG∩BC=B,AF∩AD=A,∴平面BGC∥平面ADEF
又GC?平面BGC,
∴GC∥平面ADEF.…(5分)
(2)解:以A为原点,以射线AB、AD、AF分别为x轴、y轴、
z轴建立如图所示的坐标系,
不妨令AB=AF=4,则BG=1,DE=3,
∴G(4,0,1),C(4,4,0),E(0,4,3),
| CG |
| CE |
令
| n |
| n |
则
|
|
|
|
不妨令y=1,则
| n |
又AC⊥平面BDEG,则平面BDEG的一个法向量为
| AC |
设二面角C-GE-D的大小为θ,由图得θ为锐角,
∴cosθ=
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 13 |
∴二面角C-GE-D余弦值为
2
| ||
| 13 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
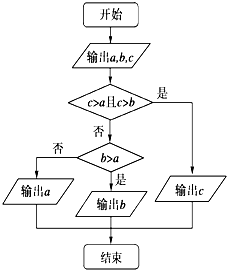 如图程序框图表示的算法是( )
如图程序框图表示的算法是( )| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
对于函数f(x)=eax-lnx(a是实常数),下列结论正确的一个是( )
A、a=1时,f(x)有极大值,且极大值点x0∈(
| ||
B、a=2时,f(x)有极小值,且极小值点x0∈(0,
| ||
C、a=
| ||
| D、a<0时,f(x)有极大值,且极大值点x0∈(-∞,0) |
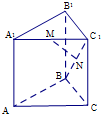 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.