题目内容
下面给出了四个类比推理:
①由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若
,
,
为三个向量则(
•
)•
=
•(
•
)”
②已知△ABC周长为c,且它的内切圆半径为r,则三角形的面积为
cr.类比推出,若四面体D-ABC的表面积为s,内切球半径为r,则其体积是
sr
③“若a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,(C为复数集)则a-b>0⇒a>b”;
④经过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2.类比上述性质,类比推出经过椭圆
+
=1上一点M(x0,y0)的切线方程为
+
=1
上述四个推理中,结论正确的是( )
①由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
②已知△ABC周长为c,且它的内切圆半径为r,则三角形的面积为
| 1 |
| 2 |
| 1 |
| 3 |
③“若a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,(C为复数集)则a-b>0⇒a>b”;
④经过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2.类比上述性质,类比推出经过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
上述四个推理中,结论正确的是( )
| A、①② | B、②③ | C、②④ | D、③④ |
考点:类比推理
专题:规律型
分析:(
•
)•
,
•(
•
)分别为与向量
,
共线的向量,当
,
方向不同时,两边不等可判断①;利用割补法,求出四面体D-ABC的体积,可判断②;根据虚数数不能比较大小,可判断③;求出过椭圆上一点的切线方程,可判断④.
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| c |
| a |
解答:
解:(
•
)•
,
•(
•
)分别为与向量
,
共线的向量,
当
,
方向不同时,两边不等,故①中推理错误;
若四面体D-ABC的四个面面积分别为:S1,S2,S3,S4,四面体D-ABC的表面积为s=S1+S2+S3+S4,若内切球半径为r,则其体积是V=
(S1+S2+S3+S4)r=
sr,故②中推理正确;
虚数无法比较大小,故:“若a,b∈C,(C为复数集)则a-b>0⇒a>b”错误,故③中推理错误;
椭圆
+
=1上一点M(x0,y0)的切线方程为
+
=1故④中推理正确;
故四个推理中,结论正确的是②④,
故选:C
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
当
| c |
| a |
若四面体D-ABC的四个面面积分别为:S1,S2,S3,S4,四面体D-ABC的表面积为s=S1+S2+S3+S4,若内切球半径为r,则其体积是V=
| 1 |
| 3 |
| 1 |
| 3 |
虚数无法比较大小,故:“若a,b∈C,(C为复数集)则a-b>0⇒a>b”错误,故③中推理错误;
椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
故四个推理中,结论正确的是②④,
故选:C
点评:本题以命题的真假判断为载体,考查了类比推理,归纳推理的证明,难度中档.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 已知函数f(x)=sin(πx+
已知函数f(x)=sin(πx+| π |
| 6 |
| PM |
| PN |
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC中,若sin2A+sin2B>sin2C,则△ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
已知数列{an}的前n项和Sn=n2-5n+4,第k项满足5<ak<8,则k等于( )
| A、4 | B、5 | C、6 | D、7 |
已知a=12(16),b=25(7),c=33(4),则a,b,c的大小关系( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<c<a |
下列推理正确的是( )
| A、如果不买彩票,那么就不能中奖.因为你买了彩票,所以你一定中奖 | ||||||||||||||||||
| B、已知三个不同的平面α,β,γ,如果α⊥β,β⊥γ,那么α⊥γ | ||||||||||||||||||
C、已知非零向量
| ||||||||||||||||||
| D、如果复数z满足z2>0,则z∈R |
已知正项数列{an}中,a1=1,a2=2,2an2=an+12+an-12(n≥2),则a22等于( )
| A、16 | ||
| B、8 | ||
C、2
| ||
| D、4 |
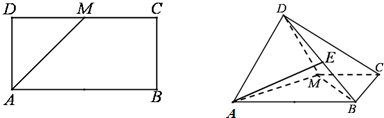 如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.