题目内容
5．已知数列{an}是等比数列，且a3=1，a5a6a7=8，则a9=（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 设等比数列{an}的公比为q，由a3=1，a5a6a7=8，可得${a}_{1}{q}^{2}$=1，${a}_{1}^{3}{q}^{15}$=8，解得q3，即可得出．
解答 解：设等比数列{an}的公比为q，∵a3=1，a5a6a7=8，
∴${a}_{1}{q}^{2}$=1，${a}_{1}^{3}{q}^{15}$=8，
解得q3=2．
则a9=${a}_{3}•{q}^{6}$=4．
点评 本题考查了等比数列的通项公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．多项式（x2-x+2）5展开式中x3的系数为（ ）
| A． | -200 | B． | -160 | C． | -120 | D． | -40 |
20．执行如图所示的程序框图．若输出的结果为3，则可输入的实数x的个数为（ ）
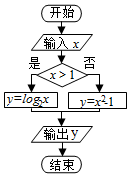
| A． | l | B． | 2 | C． | 3 | D． | 4 |
10．将4名大学生分配到A，B，C三个不同的学校实习，每个学校至少分配一人，若甲要求不到A学校，则不同的分配方案共有（ ）
| A． | 36种 | B． | 30种 | C． | 24种 | D． | 20种 |
17．已知{an}是公差为$\frac{1}{2}$的等差数列，Sn为{an}的前n项和，若a2，a6，a14成等比数列，则S5=（ ）
| A． | $\frac{35}{2}$ | B． | 35 | C． | $\frac{25}{2}$ | D． | 25 |
14．
某校高三期中考试后，数学教师对本次全部数学成绩按 1：20进行分层抽样，随机抽取了 20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如下表所示的频率分布表：
（Ⅰ）求表中 a，b 的值及成绩在[90，110）范围内的个体数，并估计这次考试全校高三数学成绩的及格率（成绩在[90，150]内为及格）；
（Ⅱ）设茎叶图中成绩在[100，120）范围内的样本的中位数为m，若从成绩在[100，120）范围内的样品中每次随机抽取1个，每次取出不放回，连续取两次，求取出两个样本中恰好一个是数字m的概率．
某校高三期中考试后，数学教师对本次全部数学成绩按 1：20进行分层抽样，随机抽取了 20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如下表所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150] | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（Ⅱ）设茎叶图中成绩在[100，120）范围内的样本的中位数为m，若从成绩在[100，120）范围内的样品中每次随机抽取1个，每次取出不放回，连续取两次，求取出两个样本中恰好一个是数字m的概率．