题目内容
15.已知数列{an}满足a1=1,an+1=$\frac{n+1}{n}$an+2n+2,则a8=120.分析 由题意可知数列{$\frac{{a}_{n}}{n}$}是以1为首项,以2为公差的等差数列,即可求出通项公式,代值计算即可.
解答 解:∵an+1=$\frac{n+1}{n}$an+2n+2,
∴$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n}$+2,
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=2,
∵a1=1,
∴$\frac{{a}_{1}}{1}$=1,
∴数列{$\frac{{a}_{n}}{n}$}是以1为首项,以2为公差的等差数列,
∴$\frac{{a}_{n}}{n}$=1+2(n-1)=2n-1,
∴an=2n2-n,
∴a8=2×82-8=120,
故答案为:120
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
5.已知数列{an}是等比数列,且a3=1,a5a6a7=8,则a9=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
4.平行直线l1:3x+4y-12=0与l2:6x+8y-15=0之间的距离为( )
| A. | $\frac{3}{10}$ | B. | $\frac{9}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{5}$ |
5.已知函数f(x)=2cos2x+sin2x-1,则以下判断中错误的是( )
| A. | 函数f(x)在区间$[{\frac{π}{8},\frac{5π}{8}}]$上是减函数 | |
| B. | 直线x=$\frac{π}{8}$是函数f(x)图象的一条对称轴 | |
| C. | 若$x∈[{0,\frac{π}{2}}]$,则函数f(x)的值域是$[{0,\sqrt{2}}]$ | |
| D. | 函数f(x)的图象可由函数y=$\sqrt{2}$sin2x的图象向左平移$\frac{π}{8}$而得到 |

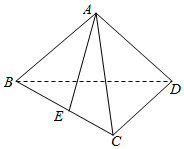 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.