题目内容

10．将4名大学生分配到A，B，C三个不同的学校实习，每个学校至少分配一人，若甲要求不到A学校，则不同的分配方案共有（　　）
A．36种B．30种C．24种D．20种

分析 根据题意中甲要求不到A学校，分析可得对甲有2种不同的分配方法，进而对剩余的三人分情况讨论，①其中有一个人与甲在同一个学校，②没有人与甲在同一个学校，易得其情况数目，最后由分步计数原理计算可得答案．

解答 解：根据题意，首先分配甲，有2种方法，
再分配其余的三人：分两种情况，①其中有一个人与甲在同一个学校，有A33=6种情况，
②没有人与甲在同一个学校，则有C32•A22=6种情况；
则若甲要求不到A学校，则不同的分配方案有2×（6+6）=24种；
故选：C．

点评 本题考查排列、组合的综合运用，注意题意中“每个学校至少分配一人”这一条件，再分配甲之后，需要对其余的三人分情况讨论．

练习册系列答案
相关题目
20．已知椭圆Γ的中心在坐标原点，且经过点$（1，\frac{3}{2}）$，它的一个焦点与抛物线E：y2=4x的焦点重合，斜率为k的直线l交抛物线E于A、B两点，交椭圆Γ于C、D两点．
（1）求椭圆Γ的方程；
（2）直线l经过点F（1，0），设点P（-1，k），且△PAB的面积为$4\sqrt{3}$，求k的值；
（3）若直线l过点M（0，-1），设直线OC，OD的斜率分别为k1，k2，且$\frac{1}{k_1}，\frac{2}{k}，\frac{1}{k_2}$成等差数列，求直线l的方程．
1．已知i为虚数单位，a∈R，若（a2+2a-3）+（a+3）i为纯虚数，则a的值为（　　）
A．1B．-3C．-3或1D．3或1
18．已知顶点在单位圆上的△ABC中，角A、B、C的对边分别为a、b、c，且2acosA=ccosB+bcosC．
（1）cosA的值；
（2）若b2+c2=4，求△ABC的面积．
5．已知数列{an}是等比数列，且a3=1，a5a6a7=8，则a9=（　　）
A．2B．4C．6D．8
15．复数$\frac{2}{（1-i）i}$（i为复数单位）的共轭复数为（　　）
A．1+iB．1-iC．-1+iD．-1-i
2．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x+5，x≤2}\\{lo{g}_{\frac{1}{2}}（x-1）+1，x＞2}\end{array}\right.$，若f（a2-3a）＞f（2a-6），则实数a的取值范围是（2，3）．
19．圆x2+y2-2x+4y-20=0截直线5x-12y+c=0的弦长为8，
（1）求c的值；
（2）求直线y=x-11上的点到圆上点的最短距离．
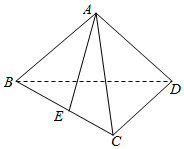20．如图，在三棱锥A-BCD中，CD⊥BD，AB=AD，E为BC的中点．
（I）求证：AE⊥BD；
（Ⅱ）设平面ABD⊥平面BCD，AD=CD=2，BC=4，求二面角B-AC-D的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网