题目内容
2.在△ABC中,内角A,B,C的对边分别为a,b,c,已知2ccosA+a=2b.(Ⅰ)求角C的值;
(Ⅱ)若c=2,求△ABC面积的最大值.
分析 (1)利用正弦定理化简2ccosA+a=2b.可得2sinCcosA+sinA=2sinB,三角形内角和定理消去B,可得角C的值;
(2)根据c=2和角C的值,利用余弦定理建立关系,结合基本不等式的性质即可求解△ABC面积的最大值.
解答 解:(1)已知2ccosA+a=2b.
正弦定理:可得2sinCcosA+sinA=2sinB,
即2sinCcosA+sinA=2sin(A+C)=2sinAcosC+2sinCcosA.
∴sinA=2sinAcosC,
∵0<A<π,sinA≠0,
∴cosC=$\frac{1}{2}$,
∵0<C<π.
∴C=$\frac{π}{3}$.
(2)∵c=2,cosC=$\frac{1}{2}$,
余弦定理,可得cosC=$\frac{1}{2}$=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$.
即a2+b2=ab+4.
∴ab+4≥2ab,当且仅当a=b时取等
∴ab≤4.
那么△ABC面积S=$\frac{1}{2}$absinC$≤2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故得△ABC面积的最大值为$\sqrt{3}$.
点评 本题考查了正余弦定理的运用和基本不等式的性质的运用和计算能力.属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
17.将23化为二进制数为( )
| A. | 10111 | B. | 10101 | C. | 11101 | D. | 00110 |
14.已知直角坐标原点O为椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的中心,F1,F2为左右焦点,在区间(0,2)任取一个数e,则事件“以e为离心率的椭圆C与圆O:x2+y2=a2-b2没有交点”的概率为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{4-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
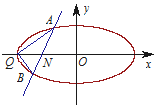 已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.
已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.