题目内容
12.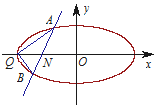 已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.
已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.(1)求椭圆C的标准方程;
(2)已知过点$(-\frac{6}{5},0)$的直线l与椭圆C交于A,B两点.
①若直线l垂直于x轴,求∠AQB的大小;
②若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.
分析 (1)利用已知条件列出a,b,c的关系,通过解方程即可得到椭圆方程.
(2)由(1)得Q(-2,0).设A(x1,y1),B(x2,y2),①当直线l垂直于x轴,求出l的方程.l的方程与C联列求解即可.②当直线l与x轴不垂直时,不存在直线l使得△QAB为等腰三角形;证明:设AB:$y=k(x+\frac{6}{5})(k≠0)$,联立直线与椭圆方程在,通过△>0,向量的数量积证明$\overrightarrow{QA}⊥\overrightarrow{QB}$,假设存在直线l使得△QAB为等腰三角形,则QA=QB.取AB的中点M,求出M的坐标,连接QM,则QM⊥AB,记点($-\frac{6}{5},0)$为N,通过向量的数量积就是$\overrightarrow{QM}$与$\overrightarrow{NM}$不垂直,得到结果.
解答 解:(1)设椭圆C的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
由题意知:$b=1,\frac{c}{a}=\frac{{\sqrt{3}}}{2},{a^2}=4$,
所以椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$. (4分)
(2)由(1)得Q(-2,0).设A(x1,y1),B(x2,y2),
①当直线l垂直于x轴,l的方程为$x=-\frac{6}{5}$,(5分)
l的方程与C联列得$A(-\frac{6}{5},\frac{4}{5}),B(-\frac{6}{5},-\frac{4}{5})$(不妨设点A在x轴上方),(6分)
此时kAQ=1,kBQ=-1,${k_{AQ}}•{K_{BQ}}=-1,∠AQB=\frac{π}{2}$(8分)
②当直线l与x轴不垂直时,不存在直线l使得△QAB为等腰三角形 (10分)
证明如下:由题意可设AB:$y=k(x+\frac{6}{5})(k≠0)$,联列方程组得(25+100k2)x2+240k2x+144k2-100=0,
显然△>0,$\overrightarrow{QA}•\overrightarrow{QB}=({x_1}+2,{y_1})•({x_2}+2,{y_2})$=$(1+{k^2}){x_1}{x_2}+(2+\frac{6}{5}{k^2})({x_1}+{x_2})+4+\frac{36}{25}{k^2}$=0,
所以$\overrightarrow{QA}⊥\overrightarrow{QB}$(12分)
假设存在直线l使得△QAB为等腰三角形,则QA=QB.取AB的中点M,${x_M}=\frac{{{x_1}+{x_2}}}{2}=-\frac{{24{k^2}}}{{5+20{k^2}}},{y_M}=k({x_M}+\frac{6}{5})=\frac{6k}{{5+20{k^2}}}$,(13分)
连接QM,则QM⊥AB,记点($-\frac{6}{5},0)$为N,所以$\overrightarrow{QM}•\overrightarrow{NM}=\frac{{60+132{k^2}}}{{{{(5+20{k^2})}^2}}}≠0$,
所以$\overrightarrow{QM}$与$\overrightarrow{NM}$不垂直,矛盾,
故不存在直线l使得△QAB为等腰三角形. (16分)
点评 本题考查椭圆方程的求法,椭圆的简单性质以及直线与椭圆的位置关系的综合应用,存在性问题的解决方法,考查分类讨论思想以及转化思想的应用,考查计算能力.

| A. | 充分非必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 必要非充分条件 |
| A. | -cos2x | B. | cos2x | C. | -sin2x | D. | sin2x |