题目内容
已知A={x||x-a|<4},B={x|
≤1}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
| 2 |
| x-1 |
(1)若a=1,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
考点:子集与交集、并集运算的转换
专题:集合
分析:(1)把a=1代入解不等式可得A={x|-3<x<5},B={x|x<1或x≥3},取交集即可;(2)由A∪B=R可得
,解不等式组可得.
|
解答:
解:(1)当a=1时,A={x||x-1|<4}={x|-3<x<5},
B={x|
≤1}={x|x<1或x≥3}.
∴A∩B={x|-3<x<1或3≤x<5};
(2)∵A={x|a-4<x<a+4},B={x|x<1或x≥3},且A∪B=R,
∴
,解得1≤a<5,
∴实数a的取值范围为:[1,5)
B={x|
| 2 |
| x-1 |
∴A∩B={x|-3<x<1或3≤x<5};
(2)∵A={x|a-4<x<a+4},B={x|x<1或x≥3},且A∪B=R,
∴
|
∴实数a的取值范围为:[1,5)
点评:本题考查集合的运算,涉及不等式的解法,属基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,S为△ABC的面积,若满足4S=a2+b2-c2,则角C=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
实数a,b,c满足a>b>c,ac<0,下列不等式一定成立的是( )
| A、c(b-a)<0 |
| B、ab2>cb2 |
| C、c(a-c)>0 |
| D、ab>ac |
在△ABC中,∠C=90°,BC=2,AC=4,AB边上点P到边AC、BC的距离乘积的取值范围是( )
| A、[0,2] | ||
| B、[0,3] | ||
| C、[0,4] | ||
D、[0,
|
已知函数f(x)=2x2+bx+c(b,c∈R)的值域为[0,+∞),若关于x的不等式f(x)<m的解集为(n,n+10),则实数m的值为( )
| A、25 | B、-25 |
| C、50 | D、-50 |
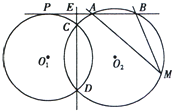 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.