题目内容
在△ABC中，∠C=90°，BC=2，AC=4，AB边上点P到边AC、BC的距离乘积的取值范围是（ ）
| A、[0，2] | ||
| B、[0，3] | ||
| C、[0，4] | ||
D、[0，
|
考点：正弦定理
专题：解三角形
分析：设PE⊥BC于E，PF⊥AC于F，由△BEP～△PFA确定
=
的关系设PE=x，PF=y，代入比例式，求得x和y的关系式，进而用y表示出xy，利用二次函数的性质求得其范围．
| BE |
| PE |
| PF |
| AF |
解答：
解：设PE⊥BC于E，PF⊥AC于F，
易证：△BEP～△PFA
∴
=
设PE=x，PF=y
则：BE=BC-CE=BC-PF=2-y
AF=AC-CF=AC-PE=4-x
所以，
=
（2-y）（4-x）=xy
8-4y-2x+xy=xy
2x+4y=8
x=4-2y
xy=y（4-2y）=-2y2+4y
所以，当y=1时，xy有最大值2，
∵xy＞0，
∴xy的范围是（0，2]．
故选：A．
易证：△BEP～△PFA
∴
| BE |
| PE |
| PF |
| AF |
设PE=x，PF=y
则：BE=BC-CE=BC-PF=2-y
AF=AC-CF=AC-PE=4-x
所以，
| 2-y |
| x |
| y |
| 4-x |
（2-y）（4-x）=xy
8-4y-2x+xy=xy
2x+4y=8
x=4-2y
xy=y（4-2y）=-2y2+4y
所以，当y=1时，xy有最大值2，
∵xy＞0，
∴xy的范围是（0，2]．
故选：A．
点评：本题主要考查了解三角形的相关问题．解题的关键时表示出xy，利用二次函数的性质解决问题．
练习册系列答案
阅读快车系列答案
相关题目
C125+C126等于（ ）
| A、C135 |
| B、C136 |
| C、C1311 |
| D、A127 |
已知m，n，l为三条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（ ）
| A、α∥β，m?α，n?β⇒m∥n |
| B、l⊥β，α⊥β⇒l∥α |
| C、m⊥α，m⊥n，⇒n∥α |
| D、α∥β，l⊥α，n?β⇒l⊥n |
设i是虚数单位，则满足i2014•z=3-4i的复数z的共轭复数是（ ）
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
已知集合A={y|y=log2x，x≥1}，B={x|y=
}，则A∩B=（ ）
| 1-x |
| A、[0，1] |
| B、（0，1） |
| C、[0，1） |
| D、（0，1] |
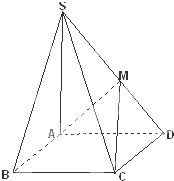如图，在四棱锥S-ABCD中，底面ABCD为矩形，SA⊥底面ABCD，M为SD的中点，且SA=AD=AB．