题目内容
设函数f(x)=x-
lnx
(1)求函数f(x)的单调递增区间;
(2)求证e2(
-
)>(
)
.
| a |
| 2 |
(1)求函数f(x)的单调递增区间;
(2)求证e2(
| π |
| e |
| π |
| e |
| e |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)f′(x)=1-
=
,分a≤0,a>0两种情况讨论,然后在定义域内解不等式f′(x)>0即可;
(2)要证e2(
-
)>(
)
,只证lne2(
-
)>ln(
)
,即证2
-
lnπ-
>0,令x=
,则2x-
lnx2-
>0,亦只证x-
lnx-
>0,构造函数利用(1)问的结论可证;
| a |
| 2x |
| 2x-a |
| 2x |
(2)要证e2(
| π |
| e |
| π |
| e |
| e |
| π |
| e |
| π |
| e |
| e |
| π |
| e |
| e |
| π |
| e |
| e |
| e |
| ||
| 2 |
解答:
解:(1)函数的定义域为(0,+∞)
f′(x)=1-
=
,
当a≤0时,f′(x)>0,f(x)的递增区间是(0,+∞);
当a>0时,由f′(x)>0,得x>
,f(x)的递增区间是(
,+∞).
综上,当a≤0时,f(x)的递增区间是(0,+∞);当a>0时,f(x)的递增区间是(
,+∞).
(2)要证e2(
-
)>(
)
,只证lne2(
-
)>ln(
)
,即证2
-
lnπ-
>0,
令x=
,则2x-
lnx2-
>0,亦只证x-
lnx-
>0,
令g(x)=x-
lnx-
,由(1)知g(x)在(
,+∞)上递增,
又
>
,
∴g(
)>g(
),即
-
ln
-
>
-
ln
-
=0.
故e2(
-
)>(
)
.
f′(x)=1-
| a |
| 2x |
| 2x-a |
| 2x |
当a≤0时,f′(x)>0,f(x)的递增区间是(0,+∞);
当a>0时,由f′(x)>0,得x>
| a |
| 2 |
| a |
| 2 |
综上,当a≤0时,f(x)的递增区间是(0,+∞);当a>0时,f(x)的递增区间是(
| a |
| 2 |
(2)要证e2(
| π |
| e |
| π |
| e |
| e |
| π |
| e |
| π |
| e |
| e |
| π |
| e |
| e |
令x=
| π |
| e |
| e |
| e |
| ||
| 2 |
令g(x)=x-
| e |
| ||
| 2 |
| e |
又
| π |
| e |
∴g(
| π |
| e |
| π |
| e |
| π |
| ||
| 2 |
| e |
| e |
| e |
| ||
| 2 |
故e2(
| π |
| e |
| π |
| e |
| e |
点评:该题考查利用导数研究函数的单调性、证明不等式,合理变形恰当构造函数是证明不等式的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、若命题p,?q都是真命题,则命题“p∧q”为真命题 |
| B、命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0则x≠0或y≠0” |
| C、命题“?x∈R,2x>0”的否定是“?x0∈R,2 x0≤0” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
设i是虚数单位,则满足i2014•z=3-4i的复数z的共轭复数是( )
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
 在正四面体ABCD中,M,N分别是BC,AD中点.
在正四面体ABCD中,M,N分别是BC,AD中点.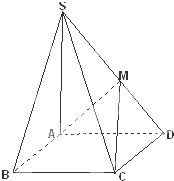 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.