题目内容
已知f(x)=x2-2ax+2.
(Ⅰ)若不等式f(x)>0在区间[2,+∞)上恒成立,求实数a的取值范围;
(Ⅱ)解关于x的不等式f(x)≤0.
(Ⅰ)若不等式f(x)>0在区间[2,+∞)上恒成立,求实数a的取值范围;
(Ⅱ)解关于x的不等式f(x)≤0.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)问题转化为2ax<x2+2在区间[2,+∞)上恒成立令g(x)=
+
,得出g(x)的最小值是
,从而求出a的范围;
(Ⅱ)先求出△=4a2-8,再分别讨论△<0,△=0,△>0时的情况,从而求出不等式的解集.
| x |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
(Ⅱ)先求出△=4a2-8,再分别讨论△<0,△=0,△>0时的情况,从而求出不等式的解集.
解答:
解:(Ⅰ)f(x)=x2-2ax+2>0 在区间[2,+∞)上恒成立,
即2ax<x2+2,
∵x≥2,∴a<
+
,
令g(x)=
+
,∴g(x)=
,
∵x≥2,∴g′(x)>0,
所以g(x)在[2,+∞)上是增函数,
所以g(x)的最小值是
.
则实数a的取值范围是(-∞,
).
(Ⅱ)∵△=4a2-8,
∴△<0,即-
<a<
时,原不等式解集为∅,
△=0,即a=±
时,原不等式对应的方程有2个不等实根,
当a=
时,原不等式的解集为{x|x=
},
当a=-
时,原不等式的解集为{x|x=-
},
△>0,即a>
或a<-
时,
原不等式对应的方程有两个不等实根,
分别为x1=a-
,x2=a+
,且x1<x2,
∴原不等式的解集为{x|a-
≤x≤a+
}.
综上,当-
<a<
时,不等式的解集为∅;
当a=
时,不等式的解集为{x|x=
};
当a=-
时,不等式的解集为{x|x=-
};
当a>
或a<-
时,不等式的解集为{x|a-
≤x≤a+
}.
即2ax<x2+2,
∵x≥2,∴a<
| x |
| 2 |
| 1 |
| x |
令g(x)=
| x |
| 2 |
| 1 |
| x |
| x2-2 |
| 2x2 |
∵x≥2,∴g′(x)>0,
所以g(x)在[2,+∞)上是增函数,
所以g(x)的最小值是
| 3 |
| 2 |
则实数a的取值范围是(-∞,
| 3 |
| 2 |
(Ⅱ)∵△=4a2-8,
∴△<0,即-
| 2 |
| 2 |
△=0,即a=±
| 2 |
当a=
| 2 |
| 2 |
当a=-
| 2 |
| 2 |
△>0,即a>
| 2 |
| 2 |
原不等式对应的方程有两个不等实根,
分别为x1=a-
| a2-2 |
| a2-2 |
∴原不等式的解集为{x|a-
| a2-2 |
| a2-2 |
综上,当-
| 2 |
| 2 |
当a=
| 2 |
| 2 |
当a=-
| 2 |
| 2 |
当a>
| 2 |
| 2 |
| a2-2 |
| a2-2 |
点评:本题考查了二次函数的性质,求参数的范围,求不等式的解集,是一道中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则( )
| x2 |
| x-1 |
| A、f(x)有极大值4 |
| B、f(x)有极小值0 |
| C、f(x)有极小值-4 |
| D、f(x)有极大值0 |
 “菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?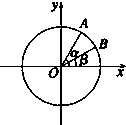 如图,在平面直角坐标系xOy中,以OX轴的非负半轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
如图,在平面直角坐标系xOy中,以OX轴的非负半轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为