题目内容
3.设集合S={0,1,2,3,…,n},则集合S中任意两个元素的差的绝对值的和为$\frac{1}{6}$n3+$\frac{1}{2}$n2+$\frac{1}{3}$n..分析 设集合S中第k个元素,则其值为k-1.然后根据数列求和进行解答.
解答 解:设集合中第k个元素,则其值为k-1.
|(k-1)-k|+|(k-1)-(k+1)|+…+|(k-1)-n|
=1+2+…+(n+1-k)
=$\frac{(n+1-k)(n+1-k+1)}{2}$
Tn=$\frac{1}{2}$n2•n+$\frac{3}{2}$n•n+n-(1+2+…+n)n-$\frac{3}{2}$(1+2+…+n)+$\frac{1}{2}$(12+22+…+n2)=$\frac{n(n+1)(n+2)}{6}=\frac{1}{6}{n^3}+\frac{1}{2}{n^2}+\frac{1}{3}n$.
故答案是:$\frac{1}{6}$n3+$\frac{1}{2}$n2+$\frac{1}{3}$n.
点评 本题考查了等差数列,数列求和,难度较大.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}$,则2y•($\frac{1}{4}$)x的最小值是( )
| A. | 1 | B. | 2 | C. | 8 | D. | 4 |
14.若函数f(x)=xlnx-ax2有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (1,2) | D. | (2,e) |
12.已知1,x,y,z,9成等比数列,则y=( )
| A. | -3 | B. | 3 | C. | 5 | D. | ±3 |
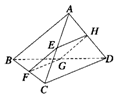 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.