题目内容
4.下列判断错误的是( )| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 若ζ~B(4,0.25),则Dξ=1 |
分析 根据不等式的基本性质,可判断A;写出原命题的否定,可判断B;根据复合命题真假判断的真值表,可判断C;根据二项分布的相关公式,计算出Dξ,可判断D.
解答 解:“am2<bm2”时,“a<b”成立,
“a<b”时,“am2<bm2”在m=0时不成立,
故“am2<bm2”是“a<b”的充分不必要条件,
故A正确;
命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$”
故B正确;
若p,q均为假命题,则p∧q为假命题,
故C正确;
若ζ~B(4,0.25),则Dξ=4×0.25×(1-0.25)=0.75;
故D错误;
故选:D
点评 本题以命题的真假判断与应用为载体,考查了充要条件,全称命题的否定,复合命题,二项分布,难度中档.

练习册系列答案
相关题目
14.若函数f(x)=xlnx-ax2有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (1,2) | D. | (2,e) |
12.已知1,x,y,z,9成等比数列,则y=( )
| A. | -3 | B. | 3 | C. | 5 | D. | ±3 |
19.设区间[q,p]的长度为p-q,其中p>q.现已知两个区间[4lnm,ln2m]与[lnm,4lnm-10]的长度相等,则ex+1+me-x的最小值为( )
| A. | 2e3 | B. | $2{e^{\frac{3}{2}}}$或2e3 | C. | $2{e^{\frac{3}{2}}}$ | D. | $2{e^{\frac{3}{2}}}$或2e2 |
9.函数y=cosx-(sinx)2+2的值域为( )
| A. | [1,3] | B. | [$\frac{1}{2}$,$\frac{11}{4}$] | C. | [$\frac{3}{4}$,3] | D. | [$\frac{3}{4}$,$\frac{11}{4}$] |
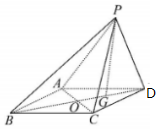 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.