题目内容
已知f(x)是定义在R上的不恒为0的函数,且对于任意的a,b∈R,都满足f(ab)=af(b)+bf(a).
(1)求f(0)、f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)(文科)若f(2)=2,un=f(2n)(n∈N*),求证:un+1>un(n∈N*).
(3)(理科)若f(2)=2,un=
(n∈N*),求数列un的前n项和Sn.
(1)求f(0)、f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)(文科)若f(2)=2,un=f(2n)(n∈N*),求证:un+1>un(n∈N*).
(3)(理科)若f(2)=2,un=
| f(2-n) |
| n |
考点:数列与函数的综合,抽象函数及其应用,数列的应用,数列的求和
专题:函数的性质及应用,等差数列与等比数列
分析:(1)令a=b=1,⇒f(1)=0;
(2)令a=b=-1⇒f(0)=0,再令a=-1,可知f(-b)=-f(b)⇒f(x)为奇函数;
(3)利用递推关系可得un+1=2un+2n+1,从而可知
-
=1,u1=f(2)=2,从而可求得un=n•2n,于是易证un+1>un(n∈N*).
(4)令tn=f(2-n)=f[(
)n],利用递推关系可求得tn=-
,继而可知un=-
,利用等比数列的求和公式即可求得答案.
(2)令a=b=-1⇒f(0)=0,再令a=-1,可知f(-b)=-f(b)⇒f(x)为奇函数;
(3)利用递推关系可得un+1=2un+2n+1,从而可知
| un+1 |
| 2n+1 |
| un |
| 2n |
(4)令tn=f(2-n)=f[(
| 1 |
| 2 |
| n |
| 2n |
| 1 |
| 2n |
解答:
解:(1)令a=b=1,则f(1)=f(1)+f(1)⇒f(1)=0;
令a=0,b=-1,则f(0)=0•f(-1)-1•f(0)⇒2f(0)=0⇒f(0)=0;
(2)令a=b=-1,则f(1)=-f(-1)-f(-1)=0⇒f(-1)=0,
令a=-1,则f(-b)=-f(b)+bf(-1)=-f(b)⇒f(x)为奇函数;
(3)(文科)un+1=f(2n+1)=f(2•2n)=2f(2n)+2nf(2)=2un+2n+1
⇒
-
=1,且u1=f(2)=2⇒
=
+(n-1)•1⇒un=n•2n
⇒
=
=
>1⇒un+1>un;
(4)(理科)令tn=f(2-n)=f[(
)n],
则tn+1=f[
(
)n]=
f[(
)n]+(
)nf(
)=
tn-(
)n+1
⇒2n+1tn+1-2ntn=-1⇒2ntn=2(-
)+(n-1)(-1)=-n
⇒tn=-
⇒un=-
⇒Sn=
=-1+
.
令a=0,b=-1,则f(0)=0•f(-1)-1•f(0)⇒2f(0)=0⇒f(0)=0;
(2)令a=b=-1,则f(1)=-f(-1)-f(-1)=0⇒f(-1)=0,
令a=-1,则f(-b)=-f(b)+bf(-1)=-f(b)⇒f(x)为奇函数;
(3)(文科)un+1=f(2n+1)=f(2•2n)=2f(2n)+2nf(2)=2un+2n+1
⇒
| un+1 |
| 2n+1 |
| un |
| 2n |
| un |
| 2n |
| 2 |
| 2 |
⇒
| un+1 |
| un |
| (n+1)•2n+1 |
| n•2n |
| (n+1)2 |
| n |
(4)(理科)令tn=f(2-n)=f[(
| 1 |
| 2 |
则tn+1=f[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
⇒2n+1tn+1-2ntn=-1⇒2ntn=2(-
| 1 |
| 2 |
⇒tn=-
| n |
| 2n |
| 1 |
| 2n |
-
| ||||
1-
|
| 1 |
| 2n |
点评:本题考查抽象函数及其应用,着重考查数列的求和与数列与函数的综合应用,考查等价转化思想与综合运算能力,属于难题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
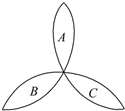 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则它在下列区间上不是减函数的是( )
| 3 |
| x |
| A、(0,+∞) |
| B、(-∞,0) |
| C、(-∞,0)∪(0,+∞) |
| D、(1,+∞) |
 如图,已知椭圆
如图,已知椭圆 如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,若它落在阴影区域内的概率为
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,若它落在阴影区域内的概率为