题目内容
已知函数f(x)=-x2+2ax+3-
a-a2(a∈R).
(Ⅰ)若函数f(x)在区间(-∞,2)上单调递增,求实数a的取值范围;
(Ⅱ)记函数y=f(x)图象的顶点为P,A(0,2),O(0,0),当∠APO最大时,求实数a的值.
| 3 |
(Ⅰ)若函数f(x)在区间(-∞,2)上单调递增,求实数a的取值范围;
(Ⅱ)记函数y=f(x)图象的顶点为P,A(0,2),O(0,0),当∠APO最大时,求实数a的值.
考点:二次函数的性质
专题:函数的性质及应用,直线与圆
分析:(Ⅰ)由抛物线f(x)=-x2+2ax+3-
a-a2开口向下,对称轴方程是x=a,在区间(-∞,2)上为增函数,能求出实数a的取值范围.
(Ⅱ)求出抛物线顶点坐标的轨迹,并分析其轨迹与以A,O为直径圆的位置关系,可分析出当∠APO最大时,顶点P的位置,进而得到P点坐标,求出实数a的值.
| 3 |
(Ⅱ)求出抛物线顶点坐标的轨迹,并分析其轨迹与以A,O为直径圆的位置关系,可分析出当∠APO最大时,顶点P的位置,进而得到P点坐标,求出实数a的值.
解答:
解:(Ⅰ)∵抛物线f(x)=-x2+2ax+3-
a-a2开口向下,
对称轴方程是x=a,
在区间(-∞,2)上为减函数,
∴a≥2,
故实数a的取值范围为:[2,+∞).
(Ⅱ)∵函数y=f(x)图象的顶点为P坐标为(a,3-
a)
则P点为直线y=-
x+3上的动点
又∵A(0,2),O(0,0),
故以AO为直径的圆C,圆心为(0,1),半径为1
点C到直线y=-
x+3的距离d=1,
即直线y=-
x+3与圆C相切
故P为切点时,∠APO最大
由
得
故a=
| 3 |
对称轴方程是x=a,
在区间(-∞,2)上为减函数,
∴a≥2,
故实数a的取值范围为:[2,+∞).
(Ⅱ)∵函数y=f(x)图象的顶点为P坐标为(a,3-
| 3 |
则P点为直线y=-
| 3 |
又∵A(0,2),O(0,0),
故以AO为直径的圆C,圆心为(0,1),半径为1
点C到直线y=-
| 3 |
即直线y=-
| 3 |
故P为切点时,∠APO最大
由
|
|
故a=
| ||
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,直线与圆的位置关系,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
已知向量
=(1,x),
=(x-1,2),若
∥
,则x=( )
| a |
| b |
| a |
| b |
| A、-1或2 | B、-2或1 |
| C、1或2 | D、-1或-2 |
已知函数f(x)=
,则它在下列区间上不是减函数的是( )
| 3 |
| x |
| A、(0,+∞) |
| B、(-∞,0) |
| C、(-∞,0)∪(0,+∞) |
| D、(1,+∞) |
设点P(x,y),其中x,y∈N,则满足x+y≤3的点P的个数为( )
| A、10 | B、9 | C、3 | D、无数 |
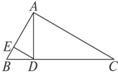 如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC= 如图,已知椭圆
如图,已知椭圆