题目内容
13．记等差数列{an}的前n项和为Sn，若a6+a10-a12=8，a14-a8=4，则S19=（ ）| A． | 224 | B． | 218 | C． | 228 | D． | 258 |
分析 利用等差数列的通项公式及其求和公式即可得出．
解答 解：设等差数列{an}的公差为d，∵a6+a10-a12=8，a14-a8=4，
∴a1+3d=8，6d=4，解得d=$\frac{2}{3}$，a1=6．
则S19=19×6+$\frac{19×18}{2}$×$\frac{2}{3}$=228．
故答案为：228．
点评 本题考查了等差数列的通项公式与求和公式及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
4．在△ABC中，若A=60°，b=4，此三角形面积S=2$\sqrt{3}$，则a的值是（ ）
| A． | 2$\sqrt{3}$ | B． | 3$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 5$\sqrt{3}$ |
1．已知f（x）=sinωx-cosωx（ω＞$\frac{1}{4}$，x∈R），若f（x）的任何一条对称轴与x轴交点的横坐标都不属于区间（2π，3π），则ω的取值范围是（ ）
| A． | [$\frac{3}{8}$，$\frac{11}{12}$]∪[$\frac{11}{8}$，$\frac{19}{12}$] | B． | （$\frac{1}{4}$，$\frac{5}{12}$]∪[$\frac{5}{8}$，$\frac{3}{4}$] | ||
| C． | [$\frac{3}{8}$，$\frac{7}{12}$]∪[$\frac{7}{8}$，$\frac{11}{12}$] | D． | （$\frac{1}{4}$，$\frac{3}{4}$]∪[$\frac{9}{8}$，$\frac{17}{12}$] |
8．设 f（x）是定义在[a-1，2]上偶函数，则f（x）=ax2+bx+1在[-2，0]上是（ ）
| A． | 增函数 | B． | 减函数 | ||
| C． | 先增后减函数 | D． | 与a，b有关，不能确定 |
18．若${log_a}\frac{4}{5}＜1$（a＞0，且a≠1），则实数a的取值范围是（ ）
| A． | $（0，\frac{4}{5}）$ | B． | $（\frac{4}{5}，+∞）$ | C． | $（\frac{4}{5}，1）$ | D． | $（0，\frac{4}{5}）∪（1，+∞）$ |
5．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，四个顶点构成的四边形的面积为4，过原点的直线l（斜率不为零）与椭圆C交于A，B两点，F1，F2为椭圆的左、右焦点，则四边形AF1BF2的周长为（ ）
| A． | 4 | B． | $4\sqrt{3}$ | C． | 8 | D． | $8\sqrt{3}$ |
2．已知函数f（x+1）是定义在R上的奇函数，若对于任意给定的不等实数x1，x2不等式（x1-x2）[f（x1）-f（x2）]＜0恒成立，则不等式f（2x-3）＞0的解集为（ ）
| A． | （0，+∞） | B． | （1，+∞） | C． | （2，+∞） | D． | （-∞，2） |
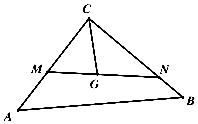如图，等腰直角三角形ABC，点G是△ABC的重心，过点G作直线与CA，CB两边分别交于M，N两点，且$\overrightarrow{CM}=λ\overrightarrow{CA}$，$\overrightarrow{CN}=μ\overrightarrow{CB}$，则λ+4μ的最小值为3．