题目内容
13.设向量$\overrightarrow a=(sinx,\sqrt{3}cosx),\overrightarrow b=(-1,1),\overrightarrow c=(1,1)$.(其中x∈[0,π])(1)若$(\overrightarrow a+\overrightarrow b)∥\overrightarrow c$,求实数x的值;
(2)若$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,求函数$sin(x+\frac{π}{6})$的值.
分析 (1)利用$(\overrightarrow a+\overrightarrow b)∥\overrightarrow c$,列出方程即可求实数x的值;
(2)由已知条件$\overrightarrow a•\overrightarrow b=\frac{1}{2}$和辅助角公式得到$sin(x+\frac{2π}{3})=\frac{1}{4}$.然后由同角三角函数关系来求$sin(x+\frac{π}{6})$的值.
解答 解:(1)∵$(\overrightarrow a+\overrightarrow b)∥\overrightarrow c⇒(sinx-1)-(\sqrt{3}cosx+1)=0$,
∴$sinx-\sqrt{3}cosx=2⇒2(\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx)=2⇒sin(x-\frac{π}{3})=1$,
又$x∈[{0,π}]⇒x-\frac{π}{3}∈[{-\frac{π}{3},\frac{2π}{3}}]$,
∴$x-\frac{π}{3}=\frac{π}{2}⇒x=\frac{5π}{6}$.
(2)∵$\overrightarrow a•\overrightarrow b=-sinx+\sqrt{3}cosx=\frac{1}{2}⇒2(-\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx)=\frac{1}{2}$,
∴$sin(x+\frac{2π}{3})=\frac{1}{4}$,
∴$sin(x+\frac{π}{6})=sin((x+\frac{2π}{3})-\frac{π}{2})=-cos(x+\frac{2π}{3})$.
又x∈[0,π]且$sin(x+\frac{2π}{3})=\frac{1}{4}>0$$⇒x+\frac{2π}{3}∈(\frac{2π}{3},π)$,
∴$cos(x+\frac{2π}{3})=-\frac{{\sqrt{15}}}{4}$即$sin(x+\frac{π}{6})=\frac{{\sqrt{15}}}{4}$.
点评 本题考查向量的共线与数量积的运算,三角函数的恒等变换应用,基本知识的考查.

 阅读快车系列答案
阅读快车系列答案| A. | 若a>b,c>d,则ac>bd | B. | 若ab≥0,则|a+b|=|a|+|b| | ||
| C. | 若x>2,则函数y=x+$\frac{1}{x}$有最小值2 | D. | 若a<b<0,则a2<ab<b2 |
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
| A. | $\frac{n}{n+1}$ | B. | $\frac{2n}{n+1}$ | C. | $\frac{n-1}{n}$ | D. | $\frac{2n-2}{n}$ |
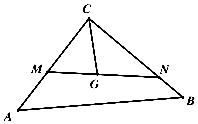 如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.
如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.


