题目内容
1.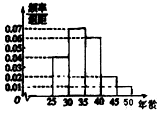 2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如图所示,并得到适龄民众对放开生育二胎政策的态度数据如表:
2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如图所示,并得到适龄民众对放开生育二胎政策的态度数据如表:| 生二胎 | 不生二胎 | 合计 | |
| 25~35岁 | 45 | 10 | 55 |
| 35~50岁 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,有多少的把握认为“生二胎与年龄有关”,说明理由;
(3)调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子,各自家庭都有一个约定:父亲先生二胎,然后儿子生二胎,则这个三个家庭“二胎出生的日期的先后顺序”有多少种?
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.076 | 3.841 | 6.635 |
分析 (1)根据题意,填写2×2列联表即可;
(2)根据调查数据计算K2,对照数表即可得出结论;
(3)分别计算三对父子的二胎出生日期仅为不同的二天、
不同的三天、不同的四天、不同的五天和不同的六天时的种数,求和即可.
解答 解:(1)根据题意,填写2×2列联表,如下:
| 生二胎 | 不生二胎 | 合计 | |
| 25~35岁 | 45 | 10 | 55 |
| 35~50岁 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
所以有90% 以上的把握认为“生二胎与年龄有关”;-------------(8分)
(3)三对父子的二胎出生日期仅为不同的二天,则有1种;
三对父子的二胎出生日期仅为不同的三天,则有${C}_{3}^{2}$${C}_{3}^{2}$${C}_{3}^{2}$-${C}_{3}^{2}$=24种;--------(9分)
三对父子的二胎出生日期仅为不同的四天,则有${C}_{4}^{2}$${C}_{4}^{2}$${C}_{4}^{2}$-${C}_{4}^{3}$×24-${C}_{4}^{2}$×1=114种;(10分)
三对父子的二胎出生日期仅为不同的五天,则有
${C}_{5}^{2}$${C}_{5}^{2}$${C}_{5}^{2}$-${C}_{5}^{4}$×114-${C}_{5}^{3}$×24-${C}_{5}^{2}$×1=180种;--------(11分)
三对父子的二胎出生日期仅为不同的六天,则有
${C}_{6}^{2}$${C}_{6}^{2}$${C}_{6}^{2}$-${C}_{6}^{5}$×180-${C}_{6}^{4}$×114-${C}_{6}^{3}$×24-${C}_{6}^{2}$×1=90或${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$=90种.
故共计有1+24+114+180+90=409种.----(12分)
(后四种每写对一种得1分)
点评 本题考查了列联表以及独立性检验的应用问题,也考查了两个计数原理的应用问题,是应用问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β下面命题正确的是( )
| A. | 若l∥β,则α∥β | B. | 若α⊥β,则l⊥m | C. | 若l⊥β,则α⊥β | D. | 若α∥β,则l∥m |
9.下列选项中,与sin2017°的值最接近的数为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{4}{5}$ |
16.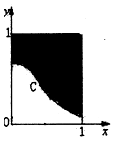 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
温馨提示:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=68.26%,P(μ-2σ<X<μ+2σ)=95.44%
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )温馨提示:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=68.26%,P(μ-2σ<X<μ+2σ)=95.44%
| A. | 7614 | B. | 6587 | C. | 6359 | D. | 3413 |
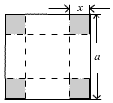 如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.
如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$. 图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )
图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )


