题目内容
数据-2，-1，2，5，6的方差是 ．
考点：极差、方差与标准差
专题：概率与统计
分析：根据方差公式计算即可．S2=
[（x1-
）2+（x2-
）2+…+（xn-
）2]．
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
解答：
解：
=
（-2-1+2+5+6）=2，
S2=
[（-2-2）2+（-1-2）2+（2-2）2+（5-2）2+（6-2）2]=10．
故答案为：10，
. |
| x |
| 1 |
| 5 |
S2=
| 1 |
| 5 |
故答案为：10，
点评：本题考查方差的定义．一般地设n个数据，x1，x2，…xn的平均数为
，则方差．S2=
[（x1-
）2+（x2-
）2+…+（xn-
）2]．它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
若正数x，y满足x2+6xy-1=0，则x+2y的最小值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
斐波那契数列{Fn}，1，1，2，3，5，8，13，21，34，55，89，144，283，…，现已知{Fn}的连续两项平方和仍是数列{Fn}中的项，则F39+F40=（ ）
| A、F39 |
| B、F40 |
| C、F41 |
| D、F42 |
设函数f（x）=
，g（x）=
，则函数f（x）•g（x）的定义域是（ ）
| 3 | 3x-2 |
| 1 | ||
|
A、[
| ||||
B、（
| ||||
C、[
| ||||
D、（
|
已知集合R为实数集，集合M={x|0＜x＜2}，N={x|x2-3x+2＞0}，则M∩∁RN=（ ）
| A、{x|0＜x＜1} |
| B、{x|1≤x＜2} |
| C、{x|1＜x＜2} |
| D、{x|0＜x＜2} |
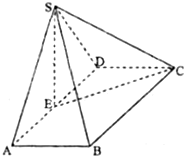如图，在四棱锥S-ABCD中，底面ABCD为矩形，侧面SAD为边长2的正三角形，且面SAD⊥面ABCD．AB=