题目内容
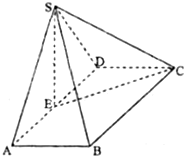 如图,在四棱锥S-ABCD中,底面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=
如图,在四棱锥S-ABCD中,底面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=| 2 |
(1)求证:BD⊥SC;
(2)求二面角E-SC-B的大小.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明BD⊥SC,先证明BD⊥面SEC,只需证明BD⊥CE,SE⊥BD;
(2)以E为原点,EA、ES所在直线分别为x轴,z轴建立坐标系,求出面ESC的法向量、面ESB的法向量,利用向量的夹角公式,即可求二面角E-SC-B的大小.
(2)以E为原点,EA、ES所在直线分别为x轴,z轴建立坐标系,求出面ESC的法向量、面ESB的法向量,利用向量的夹角公式,即可求二面角E-SC-B的大小.
解答:
 (1)证明:连接BD,设BD∩CE=O,
(1)证明:连接BD,设BD∩CE=O,
∵ED=1,CD=
,BC=2,
∴△CDE∽△BCD,∴∠DBC=∠ECD,
∵∠DBC+∠BDC=90°,∴∠ECD+∠BDC=90°,
∴∠COD=90°,∴BD⊥CE…(2分)
∵△SAD为正三角形,E为AD中点,
∴SE⊥AD,
又∵面SAD⊥面ABCD,且面SAD∩面ABCD=AD
∴SE⊥面ABCD.
∵BD?面ABCD,∴SE⊥BD,
∵BD⊥CE,SE⊥BD,CE∩SE=E,∴BD⊥面SEC,
∵SC?面SEC,∴BD⊥SC…(6分)
(2)解:如图,以E为原点,EA、ES所在直线分别为x轴,z轴建立如图所示坐标系,则A(1,0,0),B(1,
,0),C(-1,
,0),D(-1,0,0),S(0,0,
),E(0,0,0)
∴
=(-1,
,-
),
=(0,0,
),
=(1,
,-
),
设面ESC的法向量为
=(x1,y1,z1),设面ESB的法向量为
=(x2,y2,z2),则:
⊥
,
⊥
,
⊥
,
⊥
∴
,
解得:
=(
,1,0),
=(0,
,
)
∴
•
=
,|
|=
,|
|=
…(9分)
∴cos<
,
>=
=
,
∴<
,
>=arccos
设二面角E-SC-B的平面角为θ,由图可知θ=<
,
>=arccos
°
即二面角E-SC-B的大小为arccos
…(12分)
 (1)证明:连接BD,设BD∩CE=O,
(1)证明:连接BD,设BD∩CE=O,∵ED=1,CD=
| 2 |
∴△CDE∽△BCD,∴∠DBC=∠ECD,
∵∠DBC+∠BDC=90°,∴∠ECD+∠BDC=90°,
∴∠COD=90°,∴BD⊥CE…(2分)
∵△SAD为正三角形,E为AD中点,
∴SE⊥AD,
又∵面SAD⊥面ABCD,且面SAD∩面ABCD=AD
∴SE⊥面ABCD.
∵BD?面ABCD,∴SE⊥BD,
∵BD⊥CE,SE⊥BD,CE∩SE=E,∴BD⊥面SEC,
∵SC?面SEC,∴BD⊥SC…(6分)
(2)解:如图,以E为原点,EA、ES所在直线分别为x轴,z轴建立如图所示坐标系,则A(1,0,0),B(1,
| 2 |
| 2 |
| 3 |
∴
| SC |
| 2 |
| 3 |
| SE |
| 3 |
| SB |
| 2 |
| 3 |
设面ESC的法向量为
| n1 |
| n2 |
| n1 |
| SC |
| n1 |
| SE |
| n2 |
| SC |
| n2 |
| SB |
∴
|
|
解得:
| n1 |
| 2 |
| n2 |
| 3 |
| 2 |
∴
| n1 |
| n2 |
| 3 |
| n1 |
| 3 |
| n2 |
| 5 |
∴cos<
| n1 |
| n2 |
| ||||
|
| ||
| 5 |
∴<
| n1 |
| n2 |
| ||
| 5 |
设二面角E-SC-B的平面角为θ,由图可知θ=<
| n1 |
| n2 |
| ||
| 5 |
即二面角E-SC-B的大小为arccos
| ||
| 5 |
点评:本题主要考查了线面垂直的判断,以及二面角平面角的度量等有关知识,同时考查空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
运行如图的程序图,则输出s的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
若x,y满足约束条件
,则z=3x-y的取值范围是( )
|
| A、(-1,9) |
| B、[-1,9] |
| C、(1,9) |
| D、[1,9] |
在(
+
)24的展开式中,x的指数为整数的项共有( )
| 4 | x |
| 6 | |||
|
| A、3项 | B、4项 | C、5项 | D、6项 |