题目内容
19. 为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.
为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.(Ⅰ)将y表示成x的函数;
(Ⅱ)判断弧$\widehat{AB}$上是否存在一点,使建在此处的垃圾处理厂对A、B两地的总影响度最小?若存在,求出该点到A地的距离;若不存在,说明理由.
分析 (Ⅰ)$x=5\sqrt{2}$时,y=0.15,所以k=6,即可将y表示成x的函数;
(Ⅱ)利用导数,确定函数的单调性,即可得出结论.
解答 解:(I)由题意知AC⊥BC,BC2=100-x2,$y=\frac{3}{{2{x^2}}}+\frac{k}{{100-{x^2}}}(0<x<10)$,…(3分)
其中当$x=5\sqrt{2}$时,y=0.15,所以k=6,…(4分)
所以y表示成x的函数为$y=\frac{3}{{2{x^2}}}+\frac{6}{{100-{x^2}}}(0<x<10)$.…(5分)
(II)存在.由(I)知$y=\frac{3}{{2{x^2}}}+\frac{6}{{100-{x^2}}}$,
所以$y'=-\frac{3}{x^3}-\frac{6×(-2x)}{{{{(100-{x^2})}^2}}}=\frac{{12{x^4}-3{{(100-{x^2})}^2}}}{{{x^3}{{(100-{x^2})}^2}}}$,…(7分)
令y'=0得12x4=3(100-x2)2,所以${x^2}=\frac{100}{3}$,即$x=\frac{{10\sqrt{3}}}{3}$(负值舍去),…(9分)
当$0<x<\frac{{10\sqrt{3}}}{3}$时,12x4<3(100-x2)2,即y'<0,所以函数为单调减函数,…(10分)
当$\frac{{10\sqrt{3}}}{3}<x<10$时,12x4>3(100-x2)2,即y'>0,所以函数为单调增函数.…(11分)
因此当$x=\frac{{10\sqrt{3}}}{3}$时,函数$y=\frac{3}{{2{x^2}}}+\frac{6}{{100-{x^2}}}(0<x<10)$有最小值.…(12分)
即当C点到A地的距离为$\frac{{10\sqrt{3}}}{3}$km时,垃圾处理厂对两地的总影响度最小. …(13分)
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | (-∞,$\frac{1}{8}$] | B. | (0,$\frac{1}{8}$] | C. | (0,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,+∞) |
| A. | ef(2015)>f(2016) | B. | ef(2015)<f(2016) | ||
| C. | ef(2015)=f(2016) | D. | ef(2015)与f(2016)的大小不确定 |
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{1}{6}$x | C. | y=±$\frac{3}{2}$x | D. | y=±6x |
| A. | y=-x+4 | B. | y=3x | C. | y=3x-3 | D. | y=3x-9 |
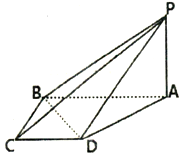 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.