题目内容
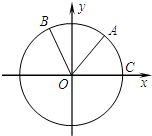 如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转| π |
| 3 |
(1)若点A的坐标为(
| 3 |
| 5 |
| 4 |
| 5 |
| 1+sin2α |
| 1+cos2α |
(2)用α表示|BC|,并求|BC|的取值范围.
考点:任意角的三角函数的定义,同角三角函数基本关系的运用,余弦定理
专题:三角函数的求值
分析:(1)由已知利用任意角的三角函数的定义可得,cosα 和sinα 的值,再利用二倍角公式求得sin2α 和 cos2α的值,可得
的值.
(2)由题意可得,|OC|=|OB|=1,∠COB=α+
,由余弦定理可得|BC|2 的解析式.根据α∈(0,
),利用余弦函数的定义域有和值域求得|BC|的范围.
| 1+sin2α |
| 1+cos2α |
(2)由题意可得,|OC|=|OB|=1,∠COB=α+
| π |
| 3 |
| π |
| 2 |
解答:
解:(1)由已知可得,cosα=
,sinα=
.
∴sin2α=2sinαcosα=
,cos2α=2cos2α-1=-
,
=
=
.
(2)由题意可得,|OC|=|OB|=1,∠COB=α+
,由余弦定理可得
|BC|2=|OC|2+|OB|2-2|OB||OC|cos∠COB=1+1-2cos(α+
)=2-2cos(α+
).
∵α∈(0,
),∴α+
∈(
,
),∴cos(α+
)∈(-
,
),
∴|BC|2∈(1,2+
),
∴|BC|∈(1,
).
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2α=2sinαcosα=
| 24 |
| 25 |
| 7 |
| 25 |
| 1+sin2α |
| 1+cos2α |
1+
| ||
1+(-
|
| 49 |
| 18 |
(2)由题意可得,|OC|=|OB|=1,∠COB=α+
| π |
| 3 |
|BC|2=|OC|2+|OB|2-2|OB||OC|cos∠COB=1+1-2cos(α+
| π |
| 3 |
| π |
| 3 |
∵α∈(0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴|BC|2∈(1,2+
| 3 |
∴|BC|∈(1,
| ||||
| 2 |
点评:本题主要考查任意角的三角函数的定义、同角三角函数的基本关系、余弦定理、二倍角公式、余弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
已知空间直线l不在平面α内,则“直线l上有两个点到平面α的距离相等”是“l∥α”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |