题目内容
若(1-
)n(n∈N*,n>1)的展开式中x-4的系数为an,则
(
+
+…+
)= .
| 1 |
| x2 |
| lim |
| n→∞ |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于-4,求得r的值,即可求得展开式中的x-4的系数an,再用裂项法求得
+
+…+
的值,从而求得所给式子的值.
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
解答:
解:(1-
)n(n∈N*,n>1)的展开式的通项公式为Tr+1=
•(-1)r•x-2r,令-2r=-4,r=2,
故展开式中x-4的系数为an=
=
,
∴
=
=2(
-
).
则
(
+
+…+
)=
2(
-
+
-
+
-
+…+
-
)=
2(1-
)=2,
故答案为:2.
| 1 |
| x2 |
| C | r n |
故展开式中x-4的系数为an=
| C | 2 n |
| n(n-1) |
| 2 |
∴
| 1 |
| an |
| 2 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
则
| lim |
| n→∞ |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| lim |
| n→∞ |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| lim |
| n→∞ |
| 1 |
| n |
故答案为:2.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,用裂项法进行数列求和,属于中档题.

练习册系列答案
相关题目
已知曲线y=x2-x上点M处的切线平行于直线x+y=1,则点M的坐标为( )
| A、(0,1) |
| B、(1,0) |
| C、(1,1) |
| D、(0,0) |
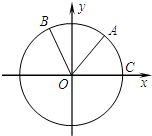 如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转