题目内容

已知tanα，tanβ是方程7x2-8x+1=0的两个根，试求tan（α+β）的值．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由条件利用一元二次方程根与系数的关系可得tanα+tanβ和tanα•tanβ的值，从而求得 tan（α+β）=
tanα+tanβ
1-tanα•tanβ
 的值．
解答： 解：由题意可得tanα+tanβ=
8
7
，tanα•tanβ=
1
7
，
∴tan（α+β）=
tanα+tanβ
1-tanα•tanβ
=
8
7
1-
1
7
=
4
3
．
点评：本题主要考查一元二次方程根与系数的关系，两角和的正切公式的应用，属于中档题．
练习册系列答案
相关题目
已知f（x）=
1-x
1+x
，若a∈（0，
π
2
），则f（cosα）+f（-cosα）可化简为
 
．
已知集合A={0，1，2，3}，B={x|x2-x=0}，则集合A∩B的子集个数为（　　）
A、2B、4C、6D、8
若数列{an}满足：a1=
2
3
，an+1-an=
2
3
(an+1+an)
，求数列的通项公式an．
已知不等式x2-（a+1）x+a＜0，
（1）若不等式在（1，3）上有解，求实数a的取值范围；
（2）若不等式在（1，3）上恒成立，求实数a的取值范围．
在等比数列{an}中，已知a1=2，且a2，a1+a3，a4成等差数列．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）设数列{an2-an}的前n项和为Sn，记bn=
2n
Sn
，求数列{bn}的前n项和Tn．
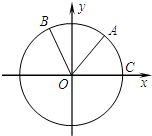如图，点A、B是单位圆O上的两点，点C是圆O与x轴的正半轴的交点，将锐角α的终边OA按逆时针方向旋转
π
3
到OB．
（1）若点A的坐标为（
3
5
，
4
5
），求
1+sin2α
1+cos2α
的值；
（2）用α表示|BC|，并求|BC|的取值范围．
如图，设圆x2+y2=12与抛物线x2=4y相交于A，B两点，F为抛物线的焦点．若过点F作一直线l交圆于点M、N，求△OMN面积的取值范围．
已知tanα=-
3
4
，则cos2α=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网