题目内容
已知圆C的圆心C(3,1),被x轴截得的弦长为4
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,求a的值.
| 2 |
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,求a的值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)利用圆C的圆心C(3,1),被x轴截得的弦长为4
,根据勾股定理求出圆的半径,即可求圆C的方程;
(2)根据圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,可得C到直线x-y+a=0的距离为
,利用点到直线的距离公式,即可求a的值.
| 2 |
(2)根据圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,可得C到直线x-y+a=0的距离为
3
| ||
| 2 |
解答:
解:(1)∵圆C的圆心C(3,1),被x轴截得的弦长为4
,
∴圆的半径为
=3,
∴圆C的方程为(x-3)2+(y-1)2=9;
(2)∵圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,
∴C到直线x-y+a=0的距离为
,
∴
=
,
∴a=1或-5.
| 2 |
∴圆的半径为
(2
|
∴圆C的方程为(x-3)2+(y-1)2=9;
(2)∵圆C与直线x-y+a=0交于A,B两点,且CA⊥CB,
∴C到直线x-y+a=0的距离为
3
| ||
| 2 |
∴
| |3-1+a| | ||
|
3
| ||
| 2 |
∴a=1或-5.
点评:本题考查圆的方程,考查点到直线的距离公式,考查学生的计算能力,正确运用点到直线的距离公式是关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
已知直线l:y=x+b,圆x2+y2=4上恰有3个点到直线l的距离都等于1,则b=( )
A、
| ||
B、-
| ||
C、±
| ||
| D、±2 |
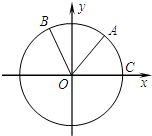 如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转 如图,设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点.若过点F作一直线l交圆于点M、N,求△OMN面积的取值范围.
如图,设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点.若过点F作一直线l交圆于点M、N,求△OMN面积的取值范围.