题目内容
某工厂有工人1000人,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样的方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1)A类工人和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表1
表2
①求x,y,再完成下列频率分布直方图;
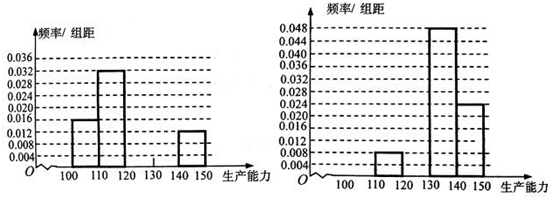
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
中的数据用该组区间的中点值作代表).
(1)A类工人和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 36 | 18 |

②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
中的数据用该组区间的中点值作代表).
考点:频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(1)根据分层抽样的特征是各层所抽取的样本数比例相等,计算出A、B类工人应抽查的人数;
(2)①根据样本容量计算出x、y的值并补充完整频率分布直方图;
②计算出A类工人和B类工人生产能力的平均数,并由此估计该工厂工人的生产能力的平均数即可.
(2)①根据样本容量计算出x、y的值并补充完整频率分布直方图;
②计算出A类工人和B类工人生产能力的平均数,并由此估计该工厂工人的生产能力的平均数即可.
解答:
解:(1)A类工人应抽查的人数是100×
=25;
B类工人应抽查的人数是100×
=75.
(2)①根据题意,由4+8+x+5+3=25,得x=5,
由6+y+36+18=75,得y=15.
补充完整频率分布直方图如下:
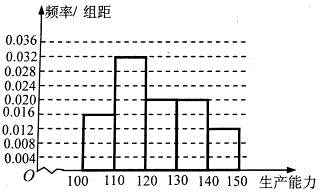 ,
,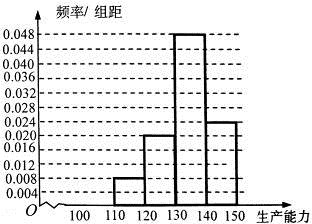 ;
;
②∵
=
×105+
×115+
×125+
×135+
×145=123,
=
×115+
×125+
×135+
×145=133.8,
∴
=
×123+
×133.8=131.1;
∴A类工人生产能力的平均数,B类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计
值分别为123,133.8,131.1.
| 250 |
| 1000 |
B类工人应抽查的人数是100×
| 750 |
| 1000 |
(2)①根据题意,由4+8+x+5+3=25,得x=5,
由6+y+36+18=75,得y=15.
补充完整频率分布直方图如下:
 ,
, ;
;②∵
. |
| xA |
| 4 |
| 25 |
| 8 |
| 25 |
| 5 |
| 25 |
| 5 |
| 25 |
| 3 |
| 25 |
. |
| xB |
| 6 |
| 75 |
| 15 |
| 75 |
| 36 |
| 75 |
| 18 |
| 75 |
∴
. |
| x |
| 25 |
| 100 |
| 75 |
| 100 |
∴A类工人生产能力的平均数,B类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计
值分别为123,133.8,131.1.
点评:本题考查了分层抽样、频率分布直方图以及求数据的平均数的问题,解题时应熟练地掌握这些知识并能灵活应用,是基础题.

练习册系列答案
相关题目
已知函数y=f(x)是定义在(-2,2)的奇函数,当x∈(0,2)时,f(x)=2x-1,则f(log2
)的值为( )
| 1 |
| 3 |
A、
| |||
B、-
| |||
| C、2 | |||
| D、-2 |
a∈(0,1),b∈(0,1),则y=log2(bx2-ax+1)的值域为R的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
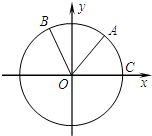 如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转
如图,点A、B是单位圆O上的两点,点C是圆O与x轴的正半轴的交点,将锐角α的终边OA按逆时针方向旋转