题目内容
投掷六个面分别记有1,2,2,3,3,3的两颗骰子
(1)求所出现的点数均为2的概率;
(2)求所出现的点数之和为4的概率.
(1)求所出现的点数均为2的概率;
(2)求所出现的点数之和为4的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)投掷六个面分别记有1,2,2,3,3,3的两颗骰子,基本事件总数n=6×6,所出现的点数均为2包含的基本事件的个数m1=2×2,由此利用等可能事件概率计算公式能求出所出现的点数均为2的概率.
(2)所出现的点数之和为4有两种情况:两颗骰子出现的点数为1,3,或两颗骰子出现的点数都为2,由此利用互斥事件概率加法公式能求出所出现的点数之和为4的概率.
(2)所出现的点数之和为4有两种情况:两颗骰子出现的点数为1,3,或两颗骰子出现的点数都为2,由此利用互斥事件概率加法公式能求出所出现的点数之和为4的概率.
解答:
解:(1)投掷六个面分别记有1,2,2,3,3,3的两颗骰子,
基本事件总数n=6×6,
所出现的点数均为2包含的基本事件的个数m1=2×2,
∴所出现的点数均为2的概率P1=
=
=
.
(2)所出现的点数之和为4有两种情况:
两颗骰子出现的点数为1,3,或两颗骰子出现的点数都为2,
∴所出现的点数之和为4的概率P2=
×
+
×
=
.
基本事件总数n=6×6,
所出现的点数均为2包含的基本事件的个数m1=2×2,
∴所出现的点数均为2的概率P1=
| m1 |
| n |
| 2×2 |
| 6×6 |
| 1 |
| 9 |
(2)所出现的点数之和为4有两种情况:
两颗骰子出现的点数为1,3,或两颗骰子出现的点数都为2,
∴所出现的点数之和为4的概率P2=
| 1 |
| 6 |
| 3 |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 7 |
| 36 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式和互斥事件概率加法公式的合理运用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
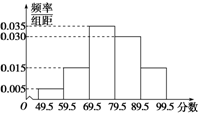 某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )
某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )| A、18篇 | B、24篇 |
| C、25篇 | D、27篇 |
函数y=x•e-x在x∈[2,4]上的最小值为( )
| A、0 | ||
B、
| ||
C、
| ||
D、
|
 对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下: