题目内容

17．函数f（x）=lg（2x-1）的定义域是（　　）
A．（1，2）B．$（{\frac{1}{2}，1}）∪（{1，+∞}）$C．$（{\frac{1}{2}，+∞}）$D．$（{\frac{1}{2}，2}）∪（{2，+∞}）$

分析 根据对数函数的性质求出函数的定义域即可．

解答 解：由题意得：2x-1＞0，解得：x＞$\frac{1}{2}$，
故函数的定义域是（$\frac{1}{2}$，+∞），
故选：C．

点评 本题考查了求函数的定义域问题，考查对数函数的性质，是一道基础题．

练习册系列答案
相关题目
7．已知实数x，y满足ax＜ay（0＜a＜1），则下列关系式恒成立的是（　　）
A．$\frac{1}{{{x^2}+1}}＞\frac{1}{{{y^2}+1}}$B．ln（x2+1）＞ln（y2+1）C．sinx＞sinyD．x3＞y3
8．抛物线16y2=x的准线方程为x=-$\frac{1}{64}$．
5．已知3∈{1，a，a-2}，则实数a的值为（　　）
A．3B．5C．3或 5D．无解
12．设m∈R，过定点A的动直线x+my=0和过定点B的直线mx-y-m+3=0，则直线AB的一般方程是3x-y=0．
2．将函数$y=sin（{2x-\frac{2π}{3}}）$的图象向左平移$\frac{π}{3}$个单位所得到的图象的解析式为（　　）
A．.y=sin2xB．.y=-sin2xC．.y=cos2xD．y=-2cosx
9．已知等比数列{an}，a1=2，a4=16
（1）求数列{an}的通项公式．
（2）求S10的值．
6．给出以下命题：
（1）“0＜t＜1”是“曲线$\frac{x^2}{t}+\frac{y^2}{1-t}=1$表示椭圆”的充要条件
（2）命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
（3）Rt△ABC中，|AC|=2，∠B=90°，∠C=30°．D是斜边AC上的点，|CD|=|CB|．以B为起点任作一条射线BE交AC于E点，则E点落在线段CD上的概率是$\frac{{\sqrt{3}}}{2}$
（4）设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=0.2，则P（-1＜ξ＜0）=0.6
则正确命题有（　　）个．
A．0B．1C．2D．3
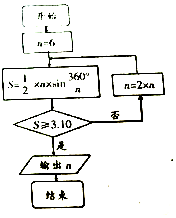7．如图是利用我国古代数学家刘徽的割圆术设计的程序框图，则输出的n值为（　　）
参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305．
A．12B．24C．48D．96

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网