题目内容
12.已知圆O1:x2+2x+y2=0,圆O2:x2-2x+y2-8=0,动圆P与圆O1外切且和圆O2内切,圆心P的轨迹为曲线C.(1)求曲线C的方程;
(2)过点(1,$\frac{1}{2}$)作直线l交曲线C于A、B两点,且点M恰好为弦AB的中点,求直线l的方程.
分析 (1)由圆的位置关系可知|PO1|+|PO2|=4,故而曲线C为以O1,O2为焦点的椭圆,根据椭圆的定义得出曲线C的方程;
(2)联立方程组,根据根与系数的关系列方程求出斜率k即可得出直线l的方程.
解答 解:(1)圆O1的圆心为O1(-1,0),半径r1=1,
圆O2的圆心为O2(1,0),半径为r2=3,
∵动圆P与圆O1外切且和圆O2内切,
∴动圆P的半径r=|PO1|-r1=r2-|PO2|,
即|PO1|+|PO2|=4,
∴P点轨迹是以O1,O2为焦点的椭圆,
∴P点轨迹曲线C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)设直线l斜率为k,则直线l的方程为:y=k(x-1)+$\frac{1}{2}$,
联立方程组$\left\{\begin{array}{l}{y=k(x-1)+\frac{1}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消元得:(3+4k2)x2+4k(1-2k)x+(2k-1)2-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{4k(2k-1)}{3+4{k}^{2}}$=2,
解得k=-$\frac{3}{2}$.
∴直线l的方程为y=-$\frac{3}{2}$(x-1)+$\frac{1}{2}$,即3x+2y-4=0.
点评 本题考查了圆的位置关系,椭圆的定义,直线与椭圆的位置关系,属于中档题.

练习册系列答案
相关题目
7.若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积等于( )
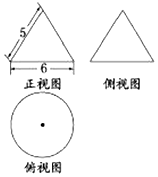

| A. | 12πcm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 30πcm2 |
17.若|x-s|<t,|y-s|<t,则下列不等式中一定成立的是( )
| A. | |x-y|<2t | B. | |x-y|<t | C. | |x-y|>2t | D. | |x-y|>t |
1.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左,右焦点分别是F1,F2,点P在双曲线上,且满足∠PF2F1=2∠PF1F2=60°,则此双曲线的离心率等于( )
| A. | 2$\sqrt{3}$-2 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
2.已知一个三棱锥的三视图如图所示,则该三棱锥的体积( )


| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
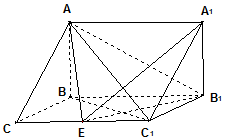 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.