题目内容
10.已知函数$f(x)=lnx-\frac{1}{2}a{x^2}-2x$(1)若函数f(x)在定义域内单调递增,求a的取值范围;
(2)若$a=-\frac{1}{2}$,且关于x的方程$f(x)=-\frac{1}{2}x+b$在[1,4]恰有两个不相等的实数根,求b的取值范围.
分析 (1)对函数f(x)进行求导,令导数大于等于0在x>0上恒成立即可.
(2)将a的值代入整理成方程的形式,然后转化为函数考虑其图象与x轴的交点的问题.
解答 解:(1)f'(x)=-$\frac{{ax}^{2}+2x-1}{x}$(x>0),
依题意f'(x)≥0 在x>0时恒成立,即ax2+2x-1≤0在x>0恒成立.
则a≤$\frac{1-2x}{{x}^{2}}$在x>0恒成立,
即a≤[($\frac{1}{x}$-1)2-1]min,x>0,
当x=1时,($\frac{1}{x}$-1)2-1取最小值-1,
∴a的取值范围是(-∞,-1];
(2)a=-$\frac{1}{2}$,f(x)=-$\frac{1}{2}$x+b,
∴$\frac{1}{4}$x2-$\frac{3}{2}$x+lnx-b=0
设g(x)=$\frac{1}{4}$x2-$\frac{3}{2}$x+lnx-b(x>0)
则g'(x)=$\frac{(x-2)(x-1)}{2x}$,
列表:
| x | (0,1) | 1 | (1,2) | 2 | (2,4) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
又g(4)=2ln2-b-2
∵方程g(x)=0在[1,4]上恰有两个不相等的实数根.
则 $\left\{\begin{array}{l}{g(1)≥0}\\{g(2)<0}\\{g(4)≥0}\end{array}\right.$,得ln2-2<b≤-$\frac{5}{4}$.
点评 本题主要考查函数单调性与其导函数正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
20.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|y=lg(x-2x2)},则A∩B=( )
| A. | [1,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$) |
1.若直线1:ax+by+1=0(a>0,b>0)把圆C:(x+4)2+(y+1)2=16分成面积相等的两部分,则当ab取得最大值时,坐标原点到直线1的距离是( )
| A. | 4 | B. | 8$\sqrt{17}$ | C. | 2 | D. | $\frac{8\sqrt{17}}{17}$ |
18.设随机变量X服从正态分布N(4,σ2),若P(X>m)=0.3,则P(X>8-m)=( )
| A. | 0.2 | B. | 0.3 | C. | 0.7 | D. | 与σ的值有关 |
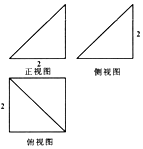
5.某几何体的三视图如图所示,则其体积为( )

| A. | 4 | B. | 8 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |