题目内容
6．《九章算术》有这样一个问题：今有男子善走，日增等里，九日走一千二百六十里，第一日、第四日、第七日所走之和为三百九十里，问第八日所走里数为（ ）| A． | 150 | B． | 160 | C． | 170 | D． | 180 |
分析 由题意可知，该男子每日走的路程构成等差数列，且a1+a4+a7=390，S9=1260，利用等差数列的性质求得a4，a5的值，进一步求得公差，则答案可求．
解答 解：由题意可知，该男子每日走的路程构成等差数列，
且a1+a4+a7=390，S9=1260，
则$\left\{\begin{array}{l}{3{a}_{4}=390}\\{9{a}_{5}=1260}\end{array}\right.$，∴a4=130，a5=140，
∴d=a5-a4=10，
则a8=a5+3d=140+30=170．
故选：C．
点评 本题考查等差数列的性质，考查了等差数列的前n项和，是基础的计算题．
练习册系列答案
相关题目
16．
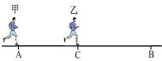如图所示，甲从A地由静止匀加速跑向B地，当甲前进距离为x1时，乙从距A地x2处的C点由静止出发，加速度与甲相同，最后二人同时到达B地，则AB两地距离为（ ）
如图所示，甲从A地由静止匀加速跑向B地，当甲前进距离为x1时，乙从距A地x2处的C点由静止出发，加速度与甲相同，最后二人同时到达B地，则AB两地距离为（ ）| A． | x1+x2 | B． | $\frac{（{x}_{1}+{x}_{2}）^{2}}{4{x}_{1}}$ | ||
| C． | $\frac{{x}_{1}^{2}}{4（{x}_{1}+{x}_{2}）}$ | D． | $\frac{（{x}_{1}+{x}_{2}）^{2}}{（{x}_{1}-{x}_{2}）{x}_{1}}$ |
10．已知正数a，b满足ab≥a+b+8则a+b的最小值为（ ）
| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
8．命题“?x≥1，x2≥1”的否定是（ ）
| A． | “?x≥1，x2＜1” | B． | “?x＜1，x2≥1” | C． | “?x0＜1，x2≥1” | D． | “?x0≥1，x2＜1” |