Question

19．作出下列各角的正弦线，余弦线，正切线：
（1）$\frac{π}{3}$；
（2）$\frac{5π}{6}$；
（3）-$\frac{2π}{3}$；
（4）-$\frac{13π}{6}$．

Answer 1

分析 作出单位圆，角的终边与单位圆交于P，过P作PM⊥x轴，交x轴于M，角的终边或终边的反向延长线交过A（1，0）且平行于y轴的直线交于点T，则MP是正弦线，OM是余弦线，AT是正切线．

解答 解：（1）$\frac{π}{3}$的终边与单位圆交于点P，与过A（1，0）且平行于y轴的直线交于点T，
过P作PM⊥x轴，交x轴于M，如下图：

则MP是正弦线，OM是余弦线，AT是正切线．
（2）$\frac{5π}{6}$的终边与单位圆交于点P，$\frac{5π}{6}$的终边的肥向延长线与过A（1，0）且平行于y轴的直线交于点T，
过P作PM⊥x轴，交x轴于M，如下图：

则MP是正弦线，OM是余弦线，AT是正切线．
（3）-$\frac{2π}{3}$的终边与单位圆交于点P，-$\frac{2π}{3}$的终边的反向延长线与过A（1，0）且平行于y轴的直线交于点T，
过P作PM⊥x轴，交x轴于M，如下图：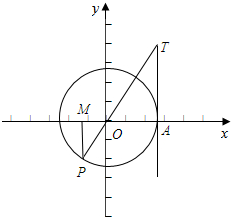

则MP是正弦线，OM是余弦线，AT是正切线．
（4）-$\frac{13π}{6}$的终边与单位圆交于点P，与过A（1，0）且平行于y轴的直线交于点T，
过P作PM⊥x轴，交x轴于M，如下图：

则MP是正弦线，OM是余弦线，AT是正切线．

点评 本题考查角的正弦线、余弦线、正切线的作法，是基础题，解题时要注意单位圆的性质的合理运用．