题目内容
3．设全集U=R，已知$A=\left\{{x\left|{\frac{2x+3}{x-2}＞0}\right.}\right\}，B=\left\{{x\left|{|{x-1}|＜2}\right.}\right\}$，则A∩B={x|2＜x＜3}．分析 先分别求出集合A和B，由此能求出A∩B．
解答 解：∵$A=\left\{{x\left|{\frac{2x+3}{x-2}＞0}\right.}\right\}，B=\left\{{x\left|{|{x-1}|＜2}\right.}\right\}$，
∴A={x|x＜-$\frac{3}{2}$或x＞2}，B={x|-1＜x＜3}，
A∩B={x|2＜x＜3}．
故答案为：{x|2＜x＜3}．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
14．若函数y=2-|x|-k有零点，则实数k的取值范围是（ ）
| A． | k∈[-1，0） | B． | k∈[0，1] | C． | k∈（0，1] | D． | k∈[0，+∞） |
11．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的离心率为2，则$\frac{b}{a}$等于（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $2\sqrt{2}$ | D． | 4 |
8．点（1，2）到直线y=x-2的距离为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{3\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | $3\sqrt{2}$ |
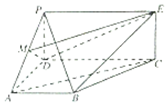如图所示的几何体中，四边形PDCE为矩形，ABCD为直角梯形，且∠BAD=∠ADC=90°，平面PDCE⊥平面ABCD，AB=AD=$\frac{1}{2}$CD=1，PD=$\sqrt{2}$．