题目内容
18．已知点A（-1，-1），B（1，3），C（1，5），D（2，7）．（1）向量$\overrightarrow{AB}$与$\overrightarrow{CD}$平行吗？
（2）向量$\overrightarrow{AC}$与$\overrightarrow{AB}$平行吗？
分析 （1）根据题意，由A、B、C、D四点的坐标计算可得向量$\overrightarrow{AB}$、$\overrightarrow{CD}$的坐标，进而分析可得$\overrightarrow{AB}$=2$\overrightarrow{CD}$，可得结论；
（2）根据题意，由A、B、C、D四点的坐标计算可得向量$\overrightarrow{AC}$、$\overrightarrow{CD}$的坐标，进而有2×4≠6×2，可以判定向量$\overrightarrow{AC}$与$\overrightarrow{AB}$不平行．
解答 解：（1）根据题意，A（-1，-1），B（1，3），C（1，5），D（2，7）．
则$\overrightarrow{AB}$=（2，4），$\overrightarrow{CD}$=（1，2）；
有$\overrightarrow{AB}$=2$\overrightarrow{CD}$；
即向量$\overrightarrow{AB}$与$\overrightarrow{CD}$平行；
（2）根据题意，A（-1，-1），B（1，3），C（1，5），D（2，7）．
则$\overrightarrow{AC}$=（2，6），$\overrightarrow{AB}$=（2，4）；
有2×4≠6×2，
故向量$\overrightarrow{AC}$与$\overrightarrow{AB}$不平行．
点评 本题考查向量平行的坐标计算，关键是利用点的坐标求出向量的坐标．
练习册系列答案
相关题目
9．已知全集U={x|x=2n，n∈Z}，集合A={-2，0，2，4}，B={-2，0，4，6，8}，则∁UA）∩B=（ ）
| A． | {2，8} | B． | {6，8} | C． | {2，4，6} | D． | {2，4，8} |
6．已知向量$\overrightarrow{AB}=（{0，2，1}）$，$\overrightarrow{AC}=（{-1，1，-2}）$，则平面ABC的一个法向量可以是（ ）
| A． | （3，-1，-2） | B． | （-4，2，2） | C． | （5，1，-2） | D． | （5，-2，1） |
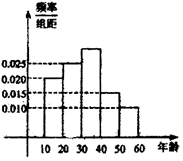某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，远离毒品”的电视公益广告，期望让更多的市民知道毒品的危害性．禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．