题目内容
12．设x，y∈R，复数z=x+yi，且满足|z|2+（z+$\overline{z}$）i=$\frac{3-i}{2+i}$，试求x，y的值．分析 把z=x+yi代入|z|2+（z+$\overline{z}$）i=$\frac{3-i}{2+i}$，整理后利用复数相等的条件列式求解x，y的值，则答案可求．
解答 解：把z=x+yi代入|z|2+（z+$\overline{z}$）i=$\frac{3-i}{2+i}$，
得${x}^{2}+{y}^{2}+2xi=\frac{（3-i）（2-i）}{（2+i）（2-i）}$=1-i，
则$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{2x=-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-\frac{\sqrt{3}}{2}}\end{array}\right.$．
点评 本题考查了复数代数形式的乘除运算，考查了复数相等的条件，考查了复数的基本概念，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
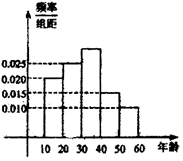某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，远离毒品”的电视公益广告，期望让更多的市民知道毒品的危害性．禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．
如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠BAD=60°，AB=2AD，PD⊥底面ABCD．